19. (8分)我们规定:对于任意实数a,b,c,d,有$[a,b]*[c,d]=ac-bd$,其中等式右边是通常的乘法和减法运算,如$[3,2]*[5,1]=3×5-2×1=13$.
(1)求$[-4,3]*[2,-6]$的值;
(2)已知关于x的方程$[x,2x-1]*[mx+1,m]=0$有两个实数根,求m的取值范围.
(1)求$[-4,3]*[2,-6]$的值;
(2)已知关于x的方程$[x,2x-1]*[mx+1,m]=0$有两个实数根,求m的取值范围.
答案:
(1)10
(2)$m\leqslant \frac{1}{4}$且$m\neq 0$
(1)10
(2)$m\leqslant \frac{1}{4}$且$m\neq 0$
20. (8分)商场服装部销售一种名牌衬衫,平均每天可售出30件,每件盈利40元.为了扩大销售、减少库存,商场决定降价销售.经调查,每件降价3元时,平均每天可多卖出6件.
(1)设降价x元,则现在每天可销售衬衫
(2)若商场要求服装部每天盈利1400元,问该种衬衫每件要降价多少元?
(3)若商场要求服装部每天盈利1600元,问这个要求能否实现?请说明理由.
(1)设降价x元,则现在每天可销售衬衫
(30+2x)
件,每件的利润是(40-x)
元(用含x的代数式表示).(2)若商场要求服装部每天盈利1400元,问该种衬衫每件要降价多少元?
若商场要求服装部每天盈利1400元,则该种衬衫每件要降价20元.
(3)若商场要求服装部每天盈利1600元,问这个要求能否实现?请说明理由.
商场要求服装部每天盈利1600元,这个要求不能实现.
答案:
(1)$(30+2x)$ $(40-x)$
(2)若商场要求服装部每天盈利1400元,则该种衬衫每件要降价20元.
(3)商场要求服装部每天盈利1600元,这个要求不能实现.
(1)$(30+2x)$ $(40-x)$
(2)若商场要求服装部每天盈利1400元,则该种衬衫每件要降价20元.
(3)商场要求服装部每天盈利1600元,这个要求不能实现.
21. (8分)我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用.例如,已知x可取任何实数,试求二次三项式$x^{2}+2x+3$的最小值.
解:$x^{2}+2x+3=x^{2}+2x+1+2=(x+1)^{2}+2$,
∵无论x取何实数,都有$(x+1)^{2}≥0$,
∴$(x+1)^{2}+2≥2$,即$x^{2}+2x+3$的最小值为2.
试利用配方法解决下列问题:
(1)直接写出$x^{2}-6x+12$的最小值为
(2)比较代数式$3x^{2}-x+2$与$2x^{2}+3x-6$的大小,并说明理由;
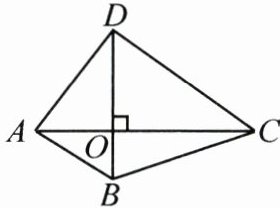
(3)如图,在四边形ABCD中,$AC⊥BD$,若$AC+BD=10$,求四边形ABCD面积的最大值.
解:$x^{2}+2x+3=x^{2}+2x+1+2=(x+1)^{2}+2$,
∵无论x取何实数,都有$(x+1)^{2}≥0$,
∴$(x+1)^{2}+2≥2$,即$x^{2}+2x+3$的最小值为2.
试利用配方法解决下列问题:
(1)直接写出$x^{2}-6x+12$的最小值为
3
;(2)比较代数式$3x^{2}-x+2$与$2x^{2}+3x-6$的大小,并说明理由;
$3x^{2}-x+2>2x^{2}+3x-6$
(3)如图,在四边形ABCD中,$AC⊥BD$,若$AC+BD=10$,求四边形ABCD面积的最大值.

四边形$ABCD$面积的最大值为$\frac{25}{2}$.
答案:
(1)3
(2)$3x^{2}-x+2>2x^{2}+3x-6$
(3)四边形$ABCD$面积的最大值为$\frac{25}{2}$.
(1)3
(2)$3x^{2}-x+2>2x^{2}+3x-6$
(3)四边形$ABCD$面积的最大值为$\frac{25}{2}$.
查看更多完整答案,请扫码查看


