14. 如图,在$▱ ABCD$中,$F$是$AD$上一点,$CF$交$BD$于点$E,CF$的延长线交$BA$的延长线于点$G,EF=1,EC=3$,则$GF$的长为____
8
.
答案:
8
15. 一块材料的形状是等腰三角形$ABC$,底边$BC=120 cm$,高$AD=120 cm$.若把这块材料加工成正方体零件(如图所示,阴影部分为正方体展开图),则正方体的表面积为__________.
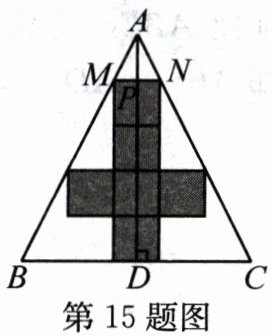

$3456cm^{2}$
答案:
$3456cm^{2}$
16. (8分)若$\frac {a}{b}=\frac {c}{d}=\frac {e}{f}=\frac {2}{5}$,
(1)若$b≠d$,求$\frac {a-c}{b-d}$的值;
(2)若$2b+3d-4f≠0$,求$\frac {2a+3c-4e}{2b+3d-4f}$的值;
(3)比较(1)(2)的结论能发现什么规律?
(1)若$b≠d$,求$\frac {a-c}{b-d}$的值;
(2)若$2b+3d-4f≠0$,求$\frac {2a+3c-4e}{2b+3d-4f}$的值;
(3)比较(1)(2)的结论能发现什么规律?
答案:
(1)$\frac{2}{5}$
(2)$\frac{2}{5}$
(3)如果$\frac{a}{b}=\frac{c}{d}=... =\frac{m}{n}(b+d+... +n≠0)$,那么$\frac{a+b+... +m}{b+d+... +n}=\frac{a}{b}$。
(1)$\frac{2}{5}$
(2)$\frac{2}{5}$
(3)如果$\frac{a}{b}=\frac{c}{d}=... =\frac{m}{n}(b+d+... +n≠0)$,那么$\frac{a+b+... +m}{b+d+... +n}=\frac{a}{b}$。
17. (8分)将图中的$\triangle ABC$作下列运动,画出相应的图形,并指出三个顶点的坐标.
(1)沿$y$轴正方向平移2个单位长度;
(2)关于$y$轴对称;
(3)以点$C$为位似中心,将$\triangle ABC$放大到原来的2倍.
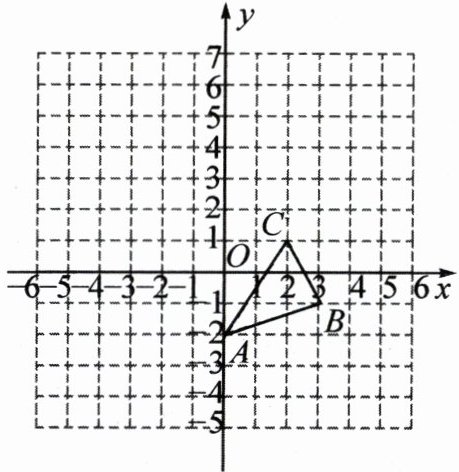
(1)沿$y$轴正方向平移2个单位长度;
(2)关于$y$轴对称;
(3)以点$C$为位似中心,将$\triangle ABC$放大到原来的2倍.

答案:
作图略。
(1)$△ABC$沿$y$轴正方向平移$2$个单位长度后所得$△A_{1}B_{1}C_{1}$的三个顶点坐标分别为$A_{1}(0,0)$,$B_{1}(3,1)$,$C_{1}(2,3)$。
(2)$△ABC$关于$y$轴对称的$△A_{2}B_{2}C_{2}$的三个顶点坐标分别为$A_{2}(0,-2)$,$B_{2}(-3,-1)$,$C_{2}(-2,1)$。
(3)将$△ABC$以点$C$为位似中心,放大为原来的$2$倍后所得$△A_{3}B_{3}C_{3}$的三个顶点坐标分别为$A_{3}(6,7)$,$B_{3}(0,5)$,$C_{3}(2,1)$或$A_{3}(-2,-5)$,$B_{3}(4,-3)$,$C_{3}(2,1)$。
(1)$△ABC$沿$y$轴正方向平移$2$个单位长度后所得$△A_{1}B_{1}C_{1}$的三个顶点坐标分别为$A_{1}(0,0)$,$B_{1}(3,1)$,$C_{1}(2,3)$。
(2)$△ABC$关于$y$轴对称的$△A_{2}B_{2}C_{2}$的三个顶点坐标分别为$A_{2}(0,-2)$,$B_{2}(-3,-1)$,$C_{2}(-2,1)$。
(3)将$△ABC$以点$C$为位似中心,放大为原来的$2$倍后所得$△A_{3}B_{3}C_{3}$的三个顶点坐标分别为$A_{3}(6,7)$,$B_{3}(0,5)$,$C_{3}(2,1)$或$A_{3}(-2,-5)$,$B_{3}(4,-3)$,$C_{3}(2,1)$。
查看更多完整答案,请扫码查看


