15. 如图,在矩形ABCD中,$AB=3$,$BC=4$,点E在边AD上,且$ED=3$,M,N分别是边AB,BC上的动点,且$BM=BN$,P是线段CE上的动点,连接PM,PN.若$PM+PN=4$,则线段PC的长为______
$ 2\sqrt{2} $
.
答案:
$ 2\sqrt{2} $
16. (8分)如图,已知矩形ABCD的对角线AC,BD相交于点O,E是边AD上的一点,连接BE,CE,OE,且$BE=CE$.求证:$\triangle BEO\cong\triangle CEO$.
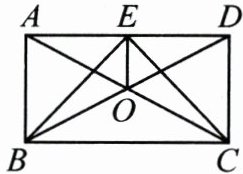

答案:
【解析】:
- 因为四边形$ABCD$是矩形,根据矩形的性质,对角线相等且互相平分,所以$OB = OC$。
- 在$\triangle BEO$和$\triangle CEO$中,已知$BE = CE$(题目所给条件),$OB = OC$(已证),$OE = OE$(公共边)。
- 根据全等三角形判定定理中的“边边边”($SSS$),可以得出$\triangle BEO\cong\triangle CEO$。
【答案】:
在矩形$ABCD$中,$OB = OC$(矩形对角线相等且互相平分)。
在$\triangle BEO$和$\triangle CEO$中,$\begin{cases}BE = CE\\OB = OC\\OE = OE\end{cases}$,所以$\triangle BEO\cong\triangle CEO(SSS)$。
- 因为四边形$ABCD$是矩形,根据矩形的性质,对角线相等且互相平分,所以$OB = OC$。
- 在$\triangle BEO$和$\triangle CEO$中,已知$BE = CE$(题目所给条件),$OB = OC$(已证),$OE = OE$(公共边)。
- 根据全等三角形判定定理中的“边边边”($SSS$),可以得出$\triangle BEO\cong\triangle CEO$。
【答案】:
在矩形$ABCD$中,$OB = OC$(矩形对角线相等且互相平分)。
在$\triangle BEO$和$\triangle CEO$中,$\begin{cases}BE = CE\\OB = OC\\OE = OE\end{cases}$,所以$\triangle BEO\cong\triangle CEO(SSS)$。
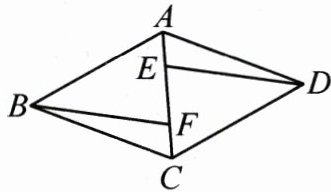
17. (8分)如图,在菱形ABCD中,E,F是对角线AC上的两点,且$AE=CF$.
(1)图中有哪几对全等三角形,请一一列举;
(2)求证:$ED// BF$.
(1)图中有哪几对全等三角形,请一一列举;
(2)求证:$ED// BF$.

答案:
(1)图中有三对全等三角形:
① $ \triangle ABC \cong \triangle CDA $;② $ \triangle ABF \cong \triangle CDE $;
③ $ \triangle ADE \cong \triangle CBF $。
(2)略
(1)图中有三对全等三角形:
① $ \triangle ABC \cong \triangle CDA $;② $ \triangle ABF \cong \triangle CDE $;
③ $ \triangle ADE \cong \triangle CBF $。
(2)略
18. (8分)如图,在四边形ABCD中,$AD// BC$,$\angle C=90^{\circ}$,$\angle ADB=\angle ABD=\frac{1}{2}\angle BDC$,DE交BC于点E,过点E作$EF\perp BD$,垂足为F,且$EF=EC$.
(1)求证:四边形ABED是菱形;
(2)若$AD=4$,求$\triangle BED$的面积.
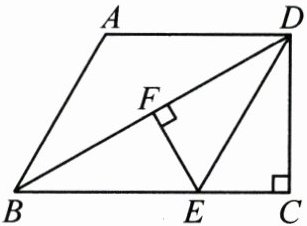
(1)求证:四边形ABED是菱形;
(2)若$AD=4$,求$\triangle BED$的面积.

答案:
(1)略
(2) $ 4\sqrt{3} $
(1)略
(2) $ 4\sqrt{3} $
查看更多完整答案,请扫码查看


