22. (10分)已知关于x的一元二次方程$x^{2}-6x+k=0$.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的一个根是$3+\sqrt {2}$,求k的值和方程的另一个根;
(3)若$x_{1},x_{2}$是这个方程的两个根,且$x_{1}^{2}+x_{2}^{2}+3x_{1}x_{2}=25$,则$k=$
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的一个根是$3+\sqrt {2}$,求k的值和方程的另一个根;
(3)若$x_{1},x_{2}$是这个方程的两个根,且$x_{1}^{2}+x_{2}^{2}+3x_{1}x_{2}=25$,则$k=$
-11
.
答案:
(1)$k<9$
(2)$k$的值为7,方程的另一个根为$3-\sqrt{2}$.
(3)$-11$
(1)$k<9$
(2)$k$的值为7,方程的另一个根为$3-\sqrt{2}$.
(3)$-11$
23. (13分)综合实践.
项目主题:草坪设计.
项目情境:某校学生参与一块长为40 m,宽为30 m的矩形草坪方案设计的项目学习,以下为项目学习小组对草坪设计的研究过程.
活动任务一:请设计两条相同宽度的小路连接矩形草坪两组对边.小组内同学们设计的方案主要有甲、乙、丙、丁四种.
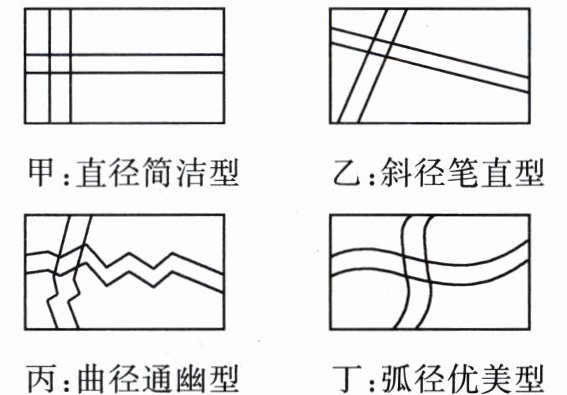
(1)探究项目小组设计出来的四种方案中小路面积的大小关系.
①直观猜想:我认为
②具体验证:选择最简单的甲、乙方案,假设小路宽为1m,则甲、乙方案中小路的面积分别为
③一般验证:若小路宽为a m,则甲、乙方案所占的面积分别为
活动任务二:为施工方便,学校选择甲种方案设计,并要求除小路后草坪面积约为$1064m^{2}$.
(2)请计算小路的宽度.
活动任务三:为了美化草坪,学校准备利用草坪上的一面墙和篱笆围(三边)成一个面积为$100m^{2}$的矩形花坛ABCD,如图所示.
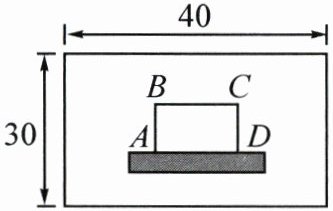
(3)为了使篱笆同时围住三面且恰好用完,项目小组的同学对下列问题展开探究,其中矩形宽$AB=x$,长$BC=y$.
①若30m长的篱笆恰好用完,请用两种不同的函数表示y关于x的函数关系.
方法1:$y=\frac{100}{x}$,
方法2:$y=30-2x$.
②若a m长的篱笆恰好用完,且有两种不同方案可以选择,使得两种方案的宽之和小于15m,甲同学说:“篱笆的长可以是28m.”乙同学说:“篱笆的长可以是32m.”你认为他们俩的说法对吗? 请说明理由.
项目主题:草坪设计.
项目情境:某校学生参与一块长为40 m,宽为30 m的矩形草坪方案设计的项目学习,以下为项目学习小组对草坪设计的研究过程.
活动任务一:请设计两条相同宽度的小路连接矩形草坪两组对边.小组内同学们设计的方案主要有甲、乙、丙、丁四种.

(1)探究项目小组设计出来的四种方案中小路面积的大小关系.
①直观猜想:我认为
四种方案中小路面积的大小相等
(请用简洁的语言或代数式表达你的猜想);②具体验证:选择最简单的甲、乙方案,假设小路宽为1m,则甲、乙方案中小路的面积分别为
69m²
和69m²
;③一般验证:若小路宽为a m,则甲、乙方案所占的面积分别为
(-a²+70a)
$m^{2}$和(-a²+70a)
$m^{2}$.活动任务二:为施工方便,学校选择甲种方案设计,并要求除小路后草坪面积约为$1064m^{2}$.
(2)请计算小路的宽度.
小路的宽为2m.
活动任务三:为了美化草坪,学校准备利用草坪上的一面墙和篱笆围(三边)成一个面积为$100m^{2}$的矩形花坛ABCD,如图所示.

(3)为了使篱笆同时围住三面且恰好用完,项目小组的同学对下列问题展开探究,其中矩形宽$AB=x$,长$BC=y$.
①若30m长的篱笆恰好用完,请用两种不同的函数表示y关于x的函数关系.
方法1:$y=\frac{100}{x}$,
方法2:$y=30-2x$.
②若a m长的篱笆恰好用完,且有两种不同方案可以选择,使得两种方案的宽之和小于15m,甲同学说:“篱笆的长可以是28m.”乙同学说:“篱笆的长可以是32m.”你认为他们俩的说法对吗? 请说明理由.
甲和乙的说法都不正确.
答案:
(1)①四种方案中小路面积的大小相等
②$69m^{2}$ $69m^{2}$ ③$(-a^{2}+70a)$ $(-a^{2}+70a)$
(2)小路的宽为$2m$.
(3)①方法1:$y=\frac{100}{x}$,
方法2:$y=30-2x$.
②甲和乙的说法都不正确.
(1)①四种方案中小路面积的大小相等
②$69m^{2}$ $69m^{2}$ ③$(-a^{2}+70a)$ $(-a^{2}+70a)$
(2)小路的宽为$2m$.
(3)①方法1:$y=\frac{100}{x}$,
方法2:$y=30-2x$.
②甲和乙的说法都不正确.
查看更多完整答案,请扫码查看


