《2025年课时A计划九年级数学上册人教版》

8. 为了减少环境污染,国家要求限制塑料玩具生产,这样有时企业会被迫停产.经过调研预测,某塑料玩具生产公司一年中每月获得的利润y(万元)和月份n之间满足函数关系式 $ y = -n^{2} + 14n - 24 $,则没有盈利的月份为
A. 2月和12月
B. 2月至12月
C. 1月
D. 1月、2月和12月

答案： D

9. 二次函数 $ y = ax^{2} - 2x + 1 $ 和一次函数 $ y = ax + a $ (a是常数,且 $ a \neq 0 $)在同一平面直角坐标系中的图象可能是

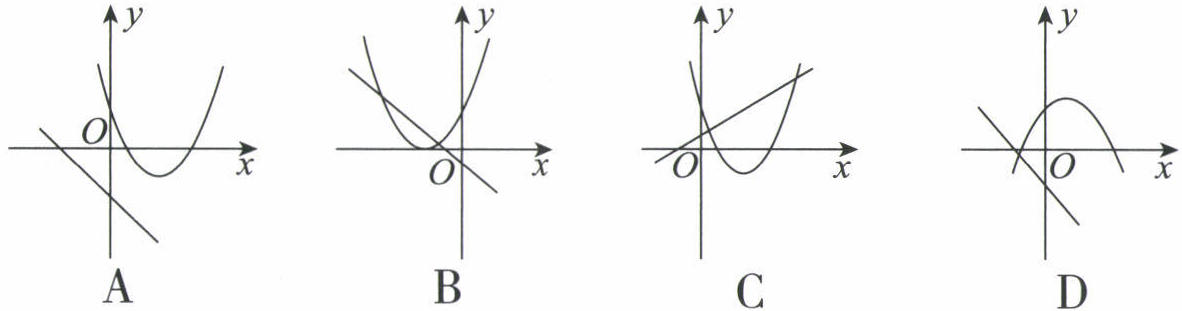
答案： C

10. 如图1,在 $ Rt\triangle ABC $ 中, $ \angle C = 90^{\circ} $,D为AC上一点, $ CD = \sqrt{2} $,动点P以每秒1个单位长度的速度从点C出发,沿 $ C \to B \to A $ 的方向匀速运动,到达点A时停止,以DP为边作正方形DPEF.设点P的运动时间为t s,正方形DPEF的面积为S,点P由点B运动到点A过程中,S关于t的函数图象如图2,则线段AB的长为

A. 7
B. $ 4\sqrt{2} $
C. $ 5\sqrt{3} $
D. 6

答案： D

11. 将抛物线 $ y = x^{2} - 2 $ 向上平移2个单位长度后的抛物线解析式为$ y = x ^ { 2 } $.

答案： $ y = x ^ { 2 } $

12. 抛物线 $ y = 2x^{2} + x - 3 $ 与x轴的交点个数为2.

答案： 2

13. 某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是 $ h = -\frac{5}{2}t^{2} + 30t + 1 $,在点火升空到最高点时引爆,则从点火升空到引爆需要的时间为6s.

答案： 6

14. 已知抛物线 $ y = x^{2} + 2(b + 1)x + c $ 经过点 $ A(2,2b - c) $.
(1)b与c之间的数量关系为$ b + c = - 4 $;
(2)过点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,若 $ AB = 2AC $,且 $ b ＜ -3 $,则抛物线的顶点坐标是$ ( 4 , - 15 ) $.

答案：
(1) $ b + c = - 4 $
(2) $ ( 4 , - 15 ) $