《2025年课时A计划九年级数学上册人教版》

21. 有同型号的A,B两把锁和同型号的a,b,c三把钥匙,其中a钥匙只能打开A锁,b钥匙只能打开B锁,c钥匙不能打开这两把锁.
(1)从三把钥匙中随机取出一把钥匙,取出c钥匙的概率等于$\frac{1}{3}$;
(2)从两把锁中随机取出一把锁,从三把钥匙中随机取出一把钥匙,求取出的钥匙恰好能打开取出

的

锁

的概率.
取出的钥匙恰好能打开取出的锁的概率为$\frac{1}{3}$.

答案：
(1)$\frac{1}{3}$.
(2)取出的钥匙恰好能打开取出的锁的概率为$\frac{1}{3}$.

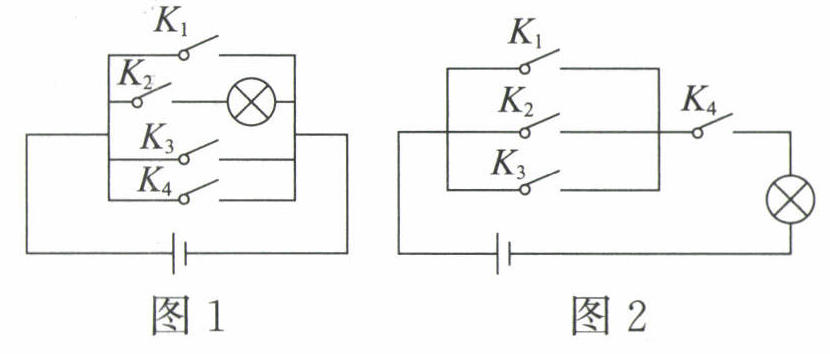
22. 已知小明设计的电路图(四个开关按键都处于打开状态)如图所示(每个开关按键闭合的可能性相等).
(1)如图1,求任意闭合一个开关按键,灯泡能发光的概率;
(2)如图2,求同时闭合其中的两个开关按键,灯泡能发光的概率.(用列表法或画树状图法)

答案：
(1)任意闭合一个开关按键,灯泡能发光的概率$=\frac{1}{4}$.
(2)同时闭合其中的两个开关按键,灯泡能发光的概率$=\frac{1}{2}$.