14. [2024·合肥蜀山区校级模拟]距离地面有一定高度的某发射装置竖直向上发射物体,物体离地面的高度h(米)与物体运动的时间t(秒)之间满足函数关系$h=-5t^{2}+mt+n$,其图象如图所示,物体运动的最高点离地面20米,物体从发射到落地的运动时间为3秒,设w表示0秒到t秒时h的值的“极差”(即0秒到t秒时h的最大值与最小值的差).
(1)$m=$
(2)当$2\leqslant t\leqslant 3$时,w的取值范围是

(1)$m=$
10
,$n=$15
;(2)当$2\leqslant t\leqslant 3$时,w的取值范围是
$5 \leq w \leq 20$
.
答案:
(1)10 15
(2)$5 \leq w \leq 20$
(1)10 15
(2)$5 \leq w \leq 20$
15. 解方程:$(x+1)^{2}=3(x+1)$.
答案:
解:$x _ { 1 } = - 1$,$x _ { 2 } = 2$。
16. 已知函数$y=kx^{2}+x+1$的图象与x轴只有一个交点,求出这个交点坐标.
答案:
解:交点坐标为$( - 1, 0 )$或$( - 2, 0 )$。
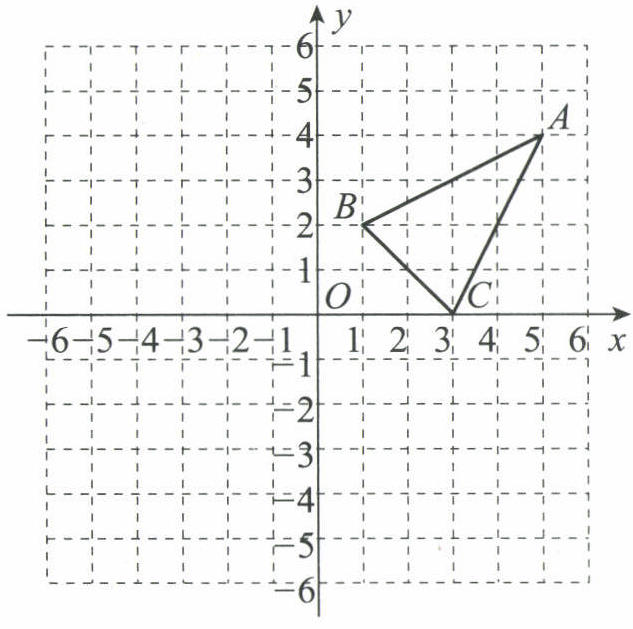
17. 如图是由边长为1个单位长度的小正方形组成的网格,$\triangle ABC$的顶点均在格点(网格线的交点)上.
(1)请画出将$\triangle ABC$向左平移6个单位长度,再向上平移1个单位长度后得到的$\triangle A_{1}B_{1}C_{1}$;
(2)画出将$\triangle ABC$绕原点O顺时针旋转$90^{\circ}$后得到的$\triangle A_{2}B_{2}C_{2}$.
(1)请画出将$\triangle ABC$向左平移6个单位长度,再向上平移1个单位长度后得到的$\triangle A_{1}B_{1}C_{1}$;
(2)画出将$\triangle ABC$绕原点O顺时针旋转$90^{\circ}$后得到的$\triangle A_{2}B_{2}C_{2}$.

答案:
本题可根据平移和旋转的性质,分别确定对应点的坐标,再顺次连接对应点得到相应图形。
$(1)$ 画出平移后的$\triangle A_{1}B_{1}C_{1}$
平移的性质为:在平面直角坐标系中,点$(x,y)$向左平移$a$个单位长度,横坐标变为$x - a$,纵坐标不变;向上平移$b$个单位长度,横坐标不变,纵坐标变为$y + b$。
已知$A(5,4)$,$B(1,2)$,$C(3,0)$,将$\triangle ABC$向左平移$6$个单位长度,再向上平移$1$个单位长度:
$A$点平移后坐标$A_1(5 - 6,4 + 1)$,即$A_1(-1,5)$;
$B$点平移后坐标$B_1(1 - 6,2 + 1)$,即$B_1(-5,3)$;
$C$点平移后坐标$C_1(3 - 6,0 + 1)$,即$C_1(-3,1)$。
在网格中找到$A_1$、$B_1$、$C_1$三点,顺次连接这三点,得到$\triangle A_{1}B_{1}C_{1}$。
$(2)$ 画出旋转后的$\triangle A_{2}B_{2}C_{2}$
旋转的性质为:在平面直角坐标系中,点$(x,y)$绕原点$O$顺时针旋转$90^{\circ}$后,其对应点的坐标变为$(y,-x)$。
$A(5,4)$绕原点$O$顺时针旋转$90^{\circ}$后,$A_2$的坐标为$(4,-5)$;
$B(1,2)$绕原点$O$顺时针旋转$90^{\circ}$后,$B_2$的坐标为$(2,-1)$;
$C(3,0)$绕原点$O$顺时针旋转$90^{\circ}$后,$C_2$的坐标为$(0,-3)$。
在网格中找到$A_2$、$B_2$、$C_2$三点,顺次连接这三点,得到$\triangle A_{2}B_{2}C_{2}$。
综上,$(1)$ 按照上述方法画出$\boldsymbol{\triangle A_{1}B_{1}C_{1}}$;$(2)$ 按照上述方法画出$\boldsymbol{\triangle A_{2}B_{2}C_{2}}$。
$(1)$ 画出平移后的$\triangle A_{1}B_{1}C_{1}$
平移的性质为:在平面直角坐标系中,点$(x,y)$向左平移$a$个单位长度,横坐标变为$x - a$,纵坐标不变;向上平移$b$个单位长度,横坐标不变,纵坐标变为$y + b$。
已知$A(5,4)$,$B(1,2)$,$C(3,0)$,将$\triangle ABC$向左平移$6$个单位长度,再向上平移$1$个单位长度:
$A$点平移后坐标$A_1(5 - 6,4 + 1)$,即$A_1(-1,5)$;
$B$点平移后坐标$B_1(1 - 6,2 + 1)$,即$B_1(-5,3)$;
$C$点平移后坐标$C_1(3 - 6,0 + 1)$,即$C_1(-3,1)$。
在网格中找到$A_1$、$B_1$、$C_1$三点,顺次连接这三点,得到$\triangle A_{1}B_{1}C_{1}$。
$(2)$ 画出旋转后的$\triangle A_{2}B_{2}C_{2}$
旋转的性质为:在平面直角坐标系中,点$(x,y)$绕原点$O$顺时针旋转$90^{\circ}$后,其对应点的坐标变为$(y,-x)$。
$A(5,4)$绕原点$O$顺时针旋转$90^{\circ}$后,$A_2$的坐标为$(4,-5)$;
$B(1,2)$绕原点$O$顺时针旋转$90^{\circ}$后,$B_2$的坐标为$(2,-1)$;
$C(3,0)$绕原点$O$顺时针旋转$90^{\circ}$后,$C_2$的坐标为$(0,-3)$。
在网格中找到$A_2$、$B_2$、$C_2$三点,顺次连接这三点,得到$\triangle A_{2}B_{2}C_{2}$。
综上,$(1)$ 按照上述方法画出$\boldsymbol{\triangle A_{1}B_{1}C_{1}}$;$(2)$ 按照上述方法画出$\boldsymbol{\triangle A_{2}B_{2}C_{2}}$。
查看更多完整答案,请扫码查看


