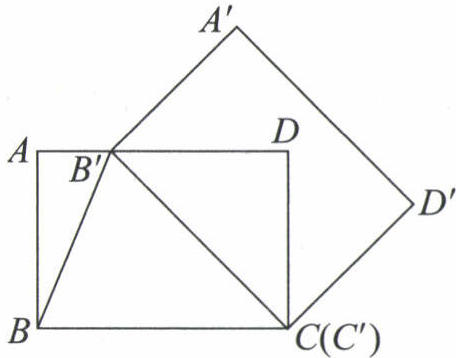
21. 如图,在矩形ABCD中,$BC=4$,将矩形ABCD绕点C顺时针旋转得到矩形$A'B'C'D'$.设旋转角为α,此时点$B'$恰好落在边AD上,连接$B'B$.
(1)当$B'$恰好是AD的中点时,求旋转角α的大小;
(2)若$∠AB'B=75^{\circ }$,求AB的长.
(1)当$B'$恰好是AD的中点时,求旋转角α的大小;
(2)若$∠AB'B=75^{\circ }$,求AB的长.

答案:
解:
(1) 当 $B'$ 恰好是 $AD$ 的中点时,旋转角 $\alpha = 60^{\circ}$。
(2) $AB = 2$。
(1) 当 $B'$ 恰好是 $AD$ 的中点时,旋转角 $\alpha = 60^{\circ}$。
(2) $AB = 2$。
22. 某公司经销一种产品,按要求必须在15天内完成销售任务.已知该产品的销售价为62元/件,推销员小李第x天的销售数量为y件,y与x满足关系:$y=\left\{\begin{array}{l} 8x(0≤x≤5),\\ 5x+10(5<x≤15).\end{array}\right.$
(1)小李第几天销售的产品数量为70件?
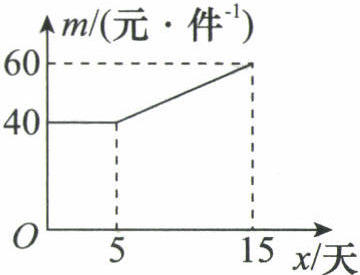
(2)设第x天销售的产品成本为m元/件,m与x的函数图象如图所示,小李第x天销售的利润为w元,求w与x的函数关系式,并求出第几天时利润最大,最大利润为多少?
(1)小李第几天销售的产品数量为70件?
(2)设第x天销售的产品成本为m元/件,m与x的函数图象如图所示,小李第x天销售的利润为w元,求w与x的函数关系式,并求出第几天时利润最大,最大利润为多少?

答案:
解:
(1) 若 $8x = 70$,得 $x = \frac{35}{4} > 5$,不符合题意,
则 $5x + 10 = 70$,解得 $x = 12$。
答:小李第 12 天销售的产品数量为 70 件。
(2) 由函数图象可知,当 $0 \leq x \leq 5$ 时,$m = 40$;
当 $5 < x \leq 15$ 时,$m = 2x + 30$。
① 当 $0 \leq x \leq 5$ 时,$w = (62 - 40)·8x = 176x$,
∵ $w$ 随 $x$ 的增大而增大,
∴ 当 $x = 5$ 时,$w$ 最大为 880;
② 当 $5 < x \leq 15$ 时,$w = (62 - 2x - 30)(5x + 10) = -10x^{2} + 140x + 320 = -10(x - 7)^{2} + 810$,
∴ 当 $x = 7$ 时,$w$ 最大为 810。
∵ $880 > 810$,
∴ 当 $x = 5$ 时,$w$ 取得最大值,为 880,
即第 5 天时利润最大,最大利润为 880 元。
(1) 若 $8x = 70$,得 $x = \frac{35}{4} > 5$,不符合题意,
则 $5x + 10 = 70$,解得 $x = 12$。
答:小李第 12 天销售的产品数量为 70 件。
(2) 由函数图象可知,当 $0 \leq x \leq 5$ 时,$m = 40$;
当 $5 < x \leq 15$ 时,$m = 2x + 30$。
① 当 $0 \leq x \leq 5$ 时,$w = (62 - 40)·8x = 176x$,
∵ $w$ 随 $x$ 的增大而增大,
∴ 当 $x = 5$ 时,$w$ 最大为 880;
② 当 $5 < x \leq 15$ 时,$w = (62 - 2x - 30)(5x + 10) = -10x^{2} + 140x + 320 = -10(x - 7)^{2} + 810$,
∴ 当 $x = 7$ 时,$w$ 最大为 810。
∵ $880 > 810$,
∴ 当 $x = 5$ 时,$w$ 取得最大值,为 880,
即第 5 天时利润最大,最大利润为 880 元。
查看更多完整答案,请扫码查看


