7. 在同一平面直角坐标系中,一次函数$y=ax+b$与二次函数$y=ax^{2}+8x+b(a≠0)$的图象可能是


答案:
C
8. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,连接AF,CE,则四边形AECF的形状不可能是

A. 平行四边形
B. 菱形
C. 矩形
D. 正方形

A. 平行四边形
B. 菱形
C. 矩形
D. 正方形
答案:
D
9. 已知抛物线$y=-x^{2}+mx$的对称轴为直线$x=2$.若关于x的一元二次方程$-x^{2}+mx-t=0$(t为实数)在$1≤x≤3$的范围内有解,则t的值不可能是
A. 2.5
B. 3
C. 3.5
D. 4
A. 2.5
B. 3
C. 3.5
D. 4
答案:
A
10. 抛物线$y=ax^{2}+bx+c(a≠0)$如图所示,下列结论错误的是
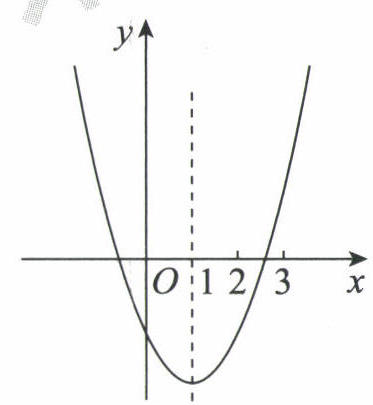
A. $2a+b=0$
B. m为任意实数时,$a+b≤m(am+b)$
C. $a-b+c<0$
D. 若$ax_{1}^{2}+bx_{1}=ax_{2}^{2}+bx_{2}$,且$x_{1}≠x_{2}$,则$x_{1}+x_{2}=2$

A. $2a+b=0$
B. m为任意实数时,$a+b≤m(am+b)$
C. $a-b+c<0$
D. 若$ax_{1}^{2}+bx_{1}=ax_{2}^{2}+bx_{2}$,且$x_{1}≠x_{2}$,则$x_{1}+x_{2}=2$
答案:
C
11. 若点$P(m,n)$与点$Q(3,-2)$关于原点对称,则$m-n=$
$-5$
.
答案:
$-5$
12. 已知方程$ax^{2}+bx+c=0$的两个解满足$x_{1}+x_{2}=2$,则抛物线$y=ax^{2}+bx+c$的对称轴为直线
$x = 1$
.
答案:
$x = 1$
13. 如图所示的图案由三个叶片组成,绕点O旋转$120^{\circ }$后可以和自身重合.若每个叶片的面积为$4cm^{2},∠AOB=120^{\circ }$,则图中阴影部分的面积之和为
4
$cm^{2}$.
答案:
4
查看更多完整答案,请扫码查看


