18. 如图,已知$△ABC$的三个顶点的坐标分别为$A(-5,0),B(-2,3),C(-1,0)$.
(1)画出$△ABC$关于原点O成中心对称的图形$△A'B'C'$;
(2)将$△ABC$绕原点O顺时针旋转$90^{\circ }$,画出对应的$△A''B''C''$,则点$B''$的坐标为____
(1)画出$△ABC$关于原点O成中心对称的图形$△A'B'C'$;
(2)将$△ABC$绕原点O顺时针旋转$90^{\circ }$,画出对应的$△A''B''C''$,则点$B''$的坐标为____
(3, 2)
.
答案:
解:
(1) 图略。
(2) 图略;$(3, 2)$。
(1) 图略。
(2) 图略;$(3, 2)$。
19. 已知关于x的一元二次方程$x^{2}+(k+3)x+3k=0$.
(1)求证:无论k取何值时,该方程总有两个实数根;
(2)若该方程有一个根大于1,求k的取值范围.
(1)求证:无论k取何值时,该方程总有两个实数根;
(2)若该方程有一个根大于1,求k的取值范围.
答案:
解:
(1) $\Delta = (k + 3)^{2} - 4×3k = (k - 3)^{2} \geq 0$,
∴无论 $k$ 取何值时,该方程总有两个实数根。
(2) $k < -1$。
(1) $\Delta = (k + 3)^{2} - 4×3k = (k - 3)^{2} \geq 0$,
∴无论 $k$ 取何值时,该方程总有两个实数根。
(2) $k < -1$。
20. 如图是一张长40 cm、宽24 cm的矩形纸板,将纸板四个角各剪去一个边长为x cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.
(1)这个无盖纸盒的长为
(2)若要制成一个底面积是$720cm^{2}$的无盖长方体纸盒,求x的值.
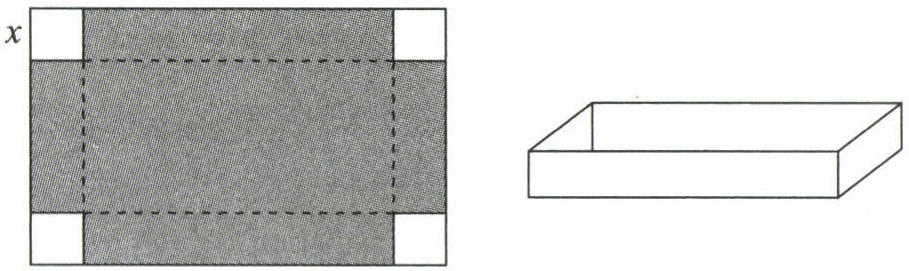
(1)这个无盖纸盒的长为
$(40 - 2x)$
cm,宽为$(24 - 2x)$
cm;(用含x的式子表示)(2)若要制成一个底面积是$720cm^{2}$的无盖长方体纸盒,求x的值.

解:(2)依题意,得$(40 - 2x)(24 - 2x) = 720$,解得$x_{1} = 2$,$x_{2} = 30$(不符合题意,舍去)。答:$x$的值为2。
答案:
解:
(1) $(40 - 2x)$;$(24 - 2x)$。
(2) 依题意,得 $(40 - 2x)(24 - 2x) = 720$,
解得 $x_{1} = 2$,$x_{2} = 30$(不符合题意,舍去)。
答:$x$ 的值为 2。
(1) $(40 - 2x)$;$(24 - 2x)$。
(2) 依题意,得 $(40 - 2x)(24 - 2x) = 720$,
解得 $x_{1} = 2$,$x_{2} = 30$(不符合题意,舍去)。
答:$x$ 的值为 2。
查看更多完整答案,请扫码查看


