《2025年名校作业七年级数学下册北师大版》

9. 下列说法正确的是 ( )
A. 三角形的角平分线、中线和高都在三角形内部
B. 直角三角形只有一条高
C. 三角形三条中线的交点一定在三角形内部
D. 三角形的高是直线，角平分线是射线，中线是线段

答案： C

10. 如图，已知BD是△ABC的中线，AB=5，BC=3，则△ABD与△BCD的周长之差是________.

答案： 2   解析：因为BD是△ABC的中线，
所以AD=CD.
所以△ABD与△BCD的周长之差是(AB+BD+AD)−(BC+BD+CD)=AB−BC=5−3=2.

【变式】如图，在△ABC中，点E是BC的中点，AB=7，AC=10，△ACE的周长是25，则△ABE的周长是________.

答案： 22      解析：因为点E是BC的中点，
所以BE=CE.
因为△ACE的周长是25，
所以AC+CE+AE=25.
因为AC=10，
所以CE+AE=15.
所以△ABE的周长为AB+BE+AE=AB+CE+AE=7+15=22.

11. 如图，在△ABC中，BO，CO分别平分∠ABC，∠ACB.若∠BOC=110°，则∠A的度数为________.

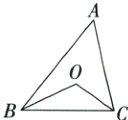
答案： 40°解析：因为∠BOC=110°，
所以∠OBC+∠OCB=180°−∠BOC=70°.
因为BO,CO分别平分∠ABC,∠ACB,
所以∠ABC=2∠OBC,∠ACB=2∠OCB.
所以∠ABC+∠ACB=2(∠OBC+∠OCB)=140°.
所以∠A=180°−(∠ABC+∠ACB)=180°−140°=40°.

12. 如图①，AD为△ABC的BC边上的中线.
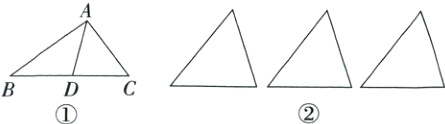
(1)试说明：$S_{\triangle ABD}=S_{\triangle ACD}$.
(2)得出结论：三角形一边上的中线把原三角形分成两个________的三角形.
(3)实际应用：如图②，学校有一块三角形空地，现需要将它分成面积相等的四部分，分别种植不同品种的花卉，请你给出三种不同的分法.

答案：
解:
(1)如图，过点A作AE⊥BC于点E.
　　　　　　　
因为点D为BC的中点，
所以BD=CD.
所以$S_{△ABD}=\frac{1}{2}BD\cdot AE$，$S_{△ACD}=\frac{1}{2}CD\cdot AE$.
所以$S_{△ABD}=S_{△ACD}$.
(2)面积相等
(3)答案不唯一，以下答案供参考.
　 　 　　

13. (1)如图①，线段AD与BC相交于点O，连接AB，CD，这样的图形我们称之为“8字形”，试说明：∠A+∠B=∠C+∠D.
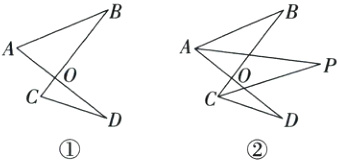
(2)如图②，在(1)的条件下，AP，CP分别平分∠BAD，∠BCD.
i)若∠B=28°，∠D=20°，求∠P的度数；
ii)当∠B和∠D为任意角时，其他条件不变，试直接写出∠P与∠B，∠D之间的数量关系.

答案：
解:
(1)在△AOB中,∠A+∠B+∠AOB=180°.
在△COD中,∠C+∠D+∠COD=180°.
因为∠AOB与∠COD是对顶角，
根据“对顶角相等”，
所以∠AOB=∠COD.
所以∠A+∠B=∠C+∠D.
(2)i)如图.
　　　　　　　
由
(1)可得∠BAD+∠B=∠BCD+∠D,
所以∠BAD−∠BCD=∠D−∠B.
因为AP,CP分别平分∠BAD,∠BCD,
所以∠1= $\frac{1}{2}$∠BAD，∠2= $\frac{1}{2}$∠BCD.
由
(1)同理,得∠P+∠2=∠B+∠1,
所以∠P=∠B+∠1−∠2=∠B+ $\frac{1}{2}$∠BAD− $\frac{1}{2}$∠BCD=∠B+ $\frac{1}{2}$(∠BAD−∠BCD)=∠B+ $\frac{1}{2}$(∠D−∠B)= $\frac{1}{2}$(∠B+∠D)=24°.
ii)∠P= $\frac{1}{2}$(∠B+∠D).

易错特训 如图，在△ABC中，BC边上的高为 ( )

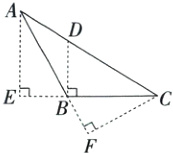
A. 线段BF
B. 线段CF
C. 线段BD
D. 线段AE

答案： 　D