《2025年名校作业七年级数学下册北师大版》

9.已知(x - 2023)²+(x - 2025)²=38，则(x - 2024)²的值为________.

答案： 18解析设x−2024=a,则x−2023=a+1,x−2025=a−1.因为(x−2023)²+(x−2025)²=38,
　所以(a+1)²+(a−1)²=38,即a²+2a+1+a²−2a+1=38.
　所以a²=18,即(x−2024)²=18.

10.计算：
(1)(3x - 2y)²+(2x + y)²；
(2)(x + 3y)²-2(x + 3y)(x - 3y)；
(3)(m - 3)²(m + 3)².

答案： 解:
(1)原式=9x²−12xy+4y²+4x²+4xy+y²
　　　　　　=13x²−8xy+5y².
(2)原式=x²+6xy+9y²−2(x²−9y²)
　　　　=x²+6xy+9y²−2x²+18y²
　　　　=−x²+6xy+27y².
(3)原式=[(m−3)(m+3)]²
　　　　　=(m²−9)²
　　　　　=m⁴−18m²+81.

11.如图，某学校有一块长为(5a + b)米，宽为(2a + b)米的长方形土地，计划在阴影部分的区域进行绿化，中间修建一个边长为(a + b)米的正方形喷水池.
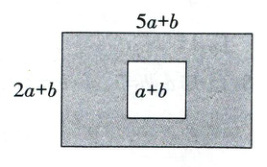
(1)绿化面积为多少平方米？(用含a,b的代数式表示)
(2)当a = 1,b = 2时，求绿化面积.

答案： 解:
(1)(5a+b)(2a+b)−(a+b)²
　　　　=10a²+5ab+2ab+b²−a²−2ab−b²
　　　　=(9a²+5ab)(平方米).
　　所以绿化面积为(9a²+5ab)平方米.
(2)当a=1,b=2时，
　　9a²+5ab=9×1²+5×1×2=19(平方米).
　　答:绿化面积为19平方米.

12.图①是一个长为2m，宽为2n的长方形，沿图中虚线剪开，得到四个相同的小长方形，然后按图②的方法拼成一个边长为m + n的正方形.

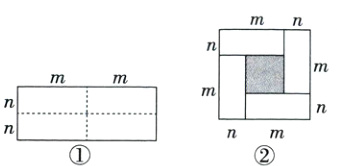
(1)请用两种不同的方法表示图②中阴影部分的面积.(用含m,n的代数式表示，不用化简)
方法1：__________________________；
方法2：__________________________.
(2)根据(1)的结果写出(m + n)²，(m - n)²，mn三个代数式之间的等量关系：________.
(3)根据(2)中你发现的等量关系，解决如下问题：若a - b = 5,ab = 6，求a + b的值.

答案： 解:
(1)(m+n)²−4mn =(m−n)²
(2)(m−n)²=(m+n)²−4mn
(3)由
(2)可得(a+b)²=(a−b)²+4ab,
　　所以(a+b)²=5²+4×6=49.
　　所以a+b=±7.