第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 下列事件中,属于必然事件的是 ( )
A. 任意抛掷一个纸杯,杯口朝下
B. $a$为有理数,$\vert a\vert\geq0$
C. 明天的气温比今天高
D. 两个负数的和是负数
A. 任意抛掷一个纸杯,杯口朝下
B. $a$为有理数,$\vert a\vert\geq0$
C. 明天的气温比今天高
D. 两个负数的和是负数
答案:
D
2. 下列说法不正确的是 ( )
A. 抛掷一枚硬币,硬币落地时正面朝上是随机事件
B. 把4个球放入两个抽屉中(每个抽屉中必须有球),其中有一个抽屉中至少有2个球是必然事件
C. 任意打开七年级下册数学教科书,正好是9页是不可能事件
D. 经过有交通信号灯的路口,遇到红灯是随机事件
A. 抛掷一枚硬币,硬币落地时正面朝上是随机事件
B. 把4个球放入两个抽屉中(每个抽屉中必须有球),其中有一个抽屉中至少有2个球是必然事件
C. 任意打开七年级下册数学教科书,正好是9页是不可能事件
D. 经过有交通信号灯的路口,遇到红灯是随机事件
答案:
C
3. 某人在做掷一枚硬币的试验时,投掷$n$次,其中正面朝上$m$次,正面朝上的频率$p = \frac{m}{n}$,下列说法中正确的是 ( )
A. $p$一定等于$\frac{1}{2}$
B. $p$一定大于$\frac{1}{2}$
C. $p$一定小于$\frac{1}{2}$
D. 随着投掷次数逐渐增加,$p$稳定在$\frac{1}{2}$附近
A. $p$一定等于$\frac{1}{2}$
B. $p$一定大于$\frac{1}{2}$
C. $p$一定小于$\frac{1}{2}$
D. 随着投掷次数逐渐增加,$p$稳定在$\frac{1}{2}$附近
答案:
D
4. 某口袋中装有红、黄、蓝三种颜色的小球(小球除颜色外完全相同)共60个. 通过大量摸球试验后,发现摸到红球、黄球的频率分别在30%和50%附近,由此估计口袋中蓝球的个数为 ( )
A. 30个
B. 18个
C. 15个
D. 12个
A. 30个
B. 18个
C. 15个
D. 12个
答案:
D 解析 由题意,得红球的个数约为60×30%=18(个),黄球的个数约为60×50%=30(个),所以估计口袋中蓝球的个数为60 - 18 - 30=12(个).
5. 在硬地上抛掷1枚图钉,通常会出现如图两种情况:

七(1)班张老师让同学们做抛掷图钉试验,每人抛掷1枚图钉20次,班长小明分别汇总了5人、10人、20人,…,的试验结果,并将获得的数据填入下表:

(1)填空:$a =$_______,$b =$_______;
(2)根据试验数据补全下面的折线统计图;
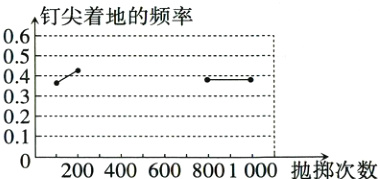
(3)估计“钉尖着地”的概率是多少.

七(1)班张老师让同学们做抛掷图钉试验,每人抛掷1枚图钉20次,班长小明分别汇总了5人、10人、20人,…,的试验结果,并将获得的数据填入下表:

(1)填空:$a =$_______,$b =$_______;
(2)根据试验数据补全下面的折线统计图;

(3)估计“钉尖着地”的概率是多少.
答案:
解:
(1)0.37 240
(2)补全折线统计图如下:

(3)通过大量试验,发现“钉尖着地”的频率在0.39附近,所以估计“钉尖着地”的概率是0.39.
解:
(1)0.37 240
(2)补全折线统计图如下:

(3)通过大量试验,发现“钉尖着地”的频率在0.39附近,所以估计“钉尖着地”的概率是0.39.
6. 如图,转盘中每个扇形的面积均相等,自由转动转盘一次,转盘停止后,指针指向的数字是奇数的概率是 ( )

A. $\frac{1}{6}$ B. $\frac{1}{3}$
C. $\frac{1}{2}$ D. $\frac{2}{3}$

A. $\frac{1}{6}$ B. $\frac{1}{3}$
C. $\frac{1}{2}$ D. $\frac{2}{3}$
答案:
D 解析 由于转盘中每个扇形的面积均相等,所以指向每个数字区域的可能性均相等.
共有6种等可能的结果,其中指向的数字是奇数的结果有4种,
所以指针指向的数字是奇数的概率是$\frac{4}{6}=\frac{2}{3}$.
共有6种等可能的结果,其中指向的数字是奇数的结果有4种,
所以指针指向的数字是奇数的概率是$\frac{4}{6}=\frac{2}{3}$.
查看更多完整答案,请扫码查看


