《2025年名校作业七年级数学下册北师大版》

1. 如图是一个可以自由转动的转盘，转盘被等分成四个扇形，转动转盘，当转盘停止时，指针落在红色区域的概率为（ ）
　　　　　　　　
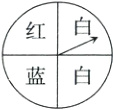
A. $\frac{1}{4}$
B. $\frac{1}{2}$
C. $\frac{3}{4}$
D. 1

答案： A

2. 如图所示的四个转盘，其中A，B两个转盘被分成8等份，若让转盘自由转动一次，停止后，指针落在阴影区域内的概率最大的是转盘______.
　

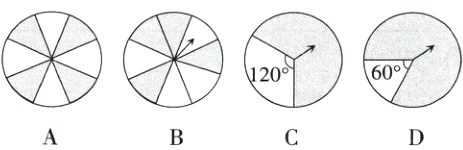
答案： D    解析A.指针落在阴影区域内的概率是$\frac{4}{8}=\frac{1}{2}$;
B.指针落在阴影区域内的概率是$\frac{4}{8}=\frac{1}{2}$;
C.指针落在阴影区域内的概率是$\frac{360^{\circ}-120^{\circ}}{360^{\circ}}=\frac{2}{3}$;
D.指针落在阴影区域内的概率是$\frac{360^{\circ}-60^{\circ}}{360^{\circ}}=\frac{5}{6}$.
因为$\frac{5}{6}＞\frac{2}{3}＞\frac{1}{2}$，
所以指针落在阴影区域内的概率最大的是转盘D.

3. 图①、图②是两个可以自由转动的转盘. 图①被分成9等份，分别标有1,2,3,4,5,6,7,8,9这九个数字. 转动转盘，当转盘停止后，指针指向的数字即为转出的数字；图②被涂上红色与绿色，绿色部分的扇形圆心角度数是120°. 转动转盘，当转盘停止后，指针指向的颜色即为转出的颜色. 小明转动图①的转盘，小亮转动图②的转盘. 小颖认为：小明转出的数字小于7的概率与小亮转出的颜色是红色的概率相同. 小颖的观点正确吗？为什么？
　　　　　　　　　　

答案： 解:正确.
理由:因为小明转出的数字共有9种等可能的结果,其中,转出的数字小于7的结果有6种,
所以小明转出的数字小于7的概率是$\frac{6}{9}=\frac{2}{3}$.
小亮转出的颜色是红色的概率是$\frac{360^{\circ}-120^{\circ}}{360^{\circ}}=\frac{2}{3}$.
因为$\frac{2}{3}=\frac{2}{3}$，
所以小颖的观点正确.

4. 如图，一个可以自由转动的转盘被过圆心的两条直线分为4份，其中α=60°，四个区域分别标有数字2,-4,6,3，任意转动转盘，停止后指针指向负数的概率是__________.
　　　　　　　　　　　　　　　　

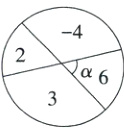
答案： $\frac{1}{3}$   解析由题意，得−4所在区域的扇形圆心角的度数为$180^{\circ}-60^{\circ}=120^{\circ}$，
所以任意转动转盘，指针指向负数的概率是$\frac{120^{\circ}}{360^{\circ}}=\frac{1}{3}$.

5. 如图，转盘的红、黄、蓝、紫四个扇形区域的圆心角分别记为α,β,γ,θ. 自由转动转盘，则下列说法正确的是__________.(填序号)
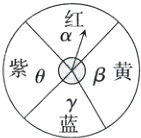
①若α=90°，则指针落在红色区域的概率为0.25
②若α - β = γ - θ，则指针落在红色和紫色区域的概率和为0.5
③若γ + θ = 200°，则指针落在红色和黄色区域的概率和小于0.5
　　　　　　　　　　　　　　　　

答案： ①②③     解析①因为$\alpha = 90^{\circ}$，
所以指针落在红色区域的概率为$\frac{\alpha}{360^{\circ}}=\frac{90^{\circ}}{360^{\circ}}=0.25$，故①正确;
②因为$\alpha-\beta=\gamma-\theta$，所以$\alpha+\theta=\beta+\gamma$.
因为$\alpha+\beta+\gamma+\theta = 360^{\circ}$，
所以$\alpha+\theta=\beta+\gamma = 180^{\circ}$.
所以指针落在红色和紫色区域的概率和为$\frac{180^{\circ}}{360^{\circ}}=0.5$，故②正确;
③因为$\gamma+\theta = 200^{\circ}$，$\alpha+\beta+\gamma+\theta = 360^{\circ}$，
所以$\alpha+\beta = 160^{\circ}$.
所以指针落在红色和黄色区域的概率和为$\frac{160^{\circ}}{360^{\circ}}＜0.5$，故③正确.

6. 如图，某商场为了吸引顾客，设立了一个可以自由转动的转盘进行抽奖，并规定：顾客每购买300元的商品就能获得一次转动转盘的机会. 转盘停止后，指针正好对准红色、绿色、黄色区域，顾客分别可以获得100元、50元、20元的购物券（转盘被等分成20个扇形），若指针恰好指在分界线上时，重新转动转盘. 已知某顾客购物320元.
（1）他获得100元、50元、20元购物券的概率分别是多少？
（2）若要让顾客获得20元购物券的概率变为$\frac{2}{5}$，则转盘无颜色的部分应怎样修改？
　　

答案： 解:
(1)由题意，得共有20种等可能的结果，其中获得100元购物券的结果有2种，获得50元购物券的结果有4种，获得20元购物券的结果有5种，
所以$P$(获得100元购物券)$=\frac{2}{20}=\frac{1}{10}$，
$P$(获得50元购物券)$=\frac{4}{20}=\frac{1}{5}$，
$P$(获得20元购物券)$=\frac{5}{20}=\frac{1}{4}$.
(2)若要让顾客获得20元购物券的概率为$\frac{2}{5}$，则黄色的扇形应该有$20\times\frac{2}{5}=8$(个).
$8 - 5 = 3$(个).
所以无颜色的部分应添加3个黄色的扇形.