《2025年全频道课时作业五年级数学下册人教版》

1. 在左右两幅图中涂色表示中间的分数。

答案：

2. 在下面的括号里填上适当的数。

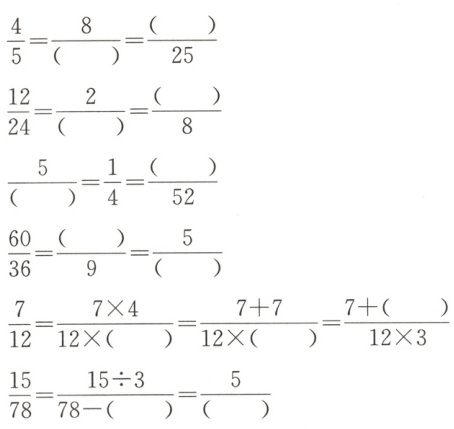
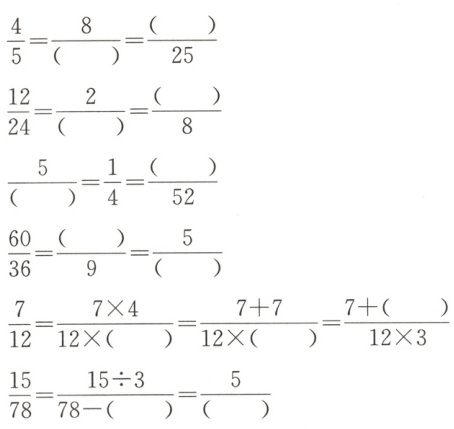
答案： 10 20 4 4 20 13 15 3 4 2 14 52 26

3. 把下面分数填在相应的圈里。
$\frac{9}{12}$ $\frac{25}{40}$ $\frac{15}{24}$ $\frac{50}{80}$ $\frac{12}{30}$ $\frac{12}{16}$
$\frac{45}{72}$ $\frac{18}{24}$ $\frac{6}{8}$
与$\frac{3}{4}$大小相等的分数 与$\frac{5}{8}$大小相等的分数

答案： 与$\frac{3}{4}$大小相等的分数：$\frac{9}{12},\frac{12}{16},\frac{18}{24},\frac{6}{8}$
与$\frac{5}{8}$大小相等的分数：$\frac{25}{40},\frac{15}{24},\frac{50}{80},\frac{45}{72}$

4. 下面哪些分数在直线上能用同一个点表示?把它们在直线上表示出来。
$\frac{5}{10}$ $\frac{3}{12}$ $\frac{9}{36}$ $\frac{3}{2}$ $\frac{12}{24}$ $\frac{42}{28}$

答案：
$\frac{3}{12}$和$\frac{9}{36}$，$\frac{5}{10}$和$\frac{12}{24}$，$\frac{3}{2}$和$\frac{42}{28}$在直线上能用同一个点表示，见下图。

5. 有8块完全相同的蛋糕，其中5块平均分给6个男生，另外3块平均分给4个女生，一个男生和一个女生相比，谁分得的蛋糕多? 多几块?

答案： $5\div6=\frac{5}{6}$(块) $3\div4=\frac{3}{4}$(块)
$\frac{3}{4}＜\frac{5}{6}$ $\frac{5}{6}-\frac{3}{4}=\frac{1}{12}$
男生分得的蛋糕多，多$\frac{1}{12}$块。

6. 一个分数的分子与分母的和是46，分子增加10后得到一个新分数，这个分数可以约分成$\frac{3}{5}$，原来的分数是多少?

答案： $46 + 10 = 56$
$\frac{3}{5}=\frac{3\times7}{5\times7}=\frac{21}{35}$ $35 + 21 = 56$ $21 - 10 = 11$
因此原来的分数是$\frac{11}{35}$。

7.[思维拓展]一个分数，它的分子与分母同时除以同一个数得$\frac{5}{7}$，原来分子与分母的和是60，原来这个分数是多少?

答案： $60\div(5 + 7)=5$
分子：$5\times5 = 25$ 分母：$5\times7 = 35$
原来这个分数是$\frac{25}{35}$。
[解析]已知原来分子与分母的和是60，现在的分子与分母的和是$5 + 7 = 12$，$60\div12 = 5$，也就是说原来的分数的分子与分母同时除以5得到$\frac{5}{7}$，把$\frac{5}{7}$的分子与分母同时乘5即可得到原来的分数。