《2025年高中阶段三测卷高一物理必修第一册人教版》

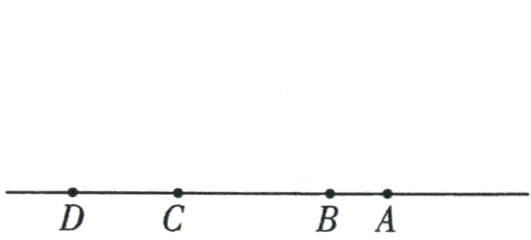
13.(9分)如图所示，一质点从O点(图中未画出)由静止出发做匀加速直线运动，依次经过图中的A、B、C、D四点，已知AB段的长度为2 m，BC段的长度为8.125 m，CD段的长度为5 m，质点从A点到B点和从C点到D点所用的时间分别为2 s和1 s。求：
(1)质点运动的加速度大小；
(2)O、D两点之间的距离。

答案：
(1)设$E$、$F$分别为$AB$、$CD$中间时刻对应的点，则质点在$AB$段和$CD$段间的平均速度分别为
$v_{E}=\frac{x_{AB}}{t_{AB}}=1$ m/s，$v_{F}=\frac{x_{CD}}{t_{CD}}=5$ m/s (2分)
则质点从$B$点到$C$点，根据匀变速直线运动公式有
$(v_{F}-\frac{at_{CD}}{2})^{2}-(v_{E}+\frac{at_{AB}}{2})^{2}=2ax_{BC}$ (2分)
联立解得$a = 1$ m/s² (1分)
(2)质点在$C$点的速度为
$v_{C}=v_{F}-\frac{at_{CD}}{2}=4.5$ m/s (1分)
质点从$O$点到$C$点，有$v_{C}^{2}=2ax_{OC}$ (1分)
解得$x_{OC}=10.125$ m (1分)
则$O$、$D$两点之间的距离为
$x_{OD}=x_{OC}+x_{CD}=15.125$ m (1分)

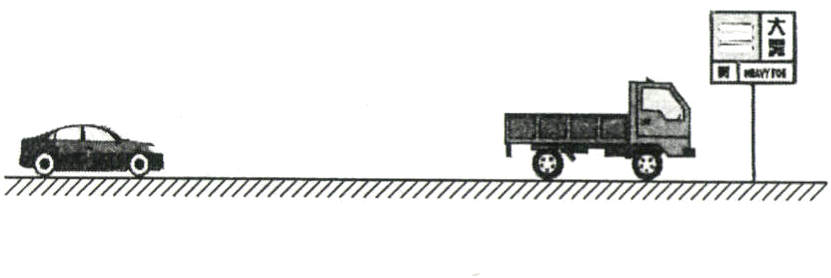
14.(14分)如图所示，某段平直单车道公路上有一辆轿车和一辆货车同向匀速行驶，其速度大小分别为v₁ = 30 m/s，v₂ = 10 m/s。由于天气有雾，轿车在其前方x₀ = 32.5 m处发现了货车，轿车司机立即刹车(忽略其反应时间)。已知轿车刹车后要经过x = 75 m才能停下来，两车均可视为质点。
(1)求轿车刹车后减速运动的加速度大小；
(2)若轿车司机立即刹车后，货车仍以速度v₂向前做匀速直线运动，试判断此过程两车是否相撞，若不相撞，求出最小距离；若相撞，写出证明过程；
(3)若大雾之前的雨水天气导致该路段变得更湿滑了，使得轿车刹车过程中的加速度减小为原来的$\frac{5}{6}$，轿车司机在距离货车x₀ = 32.5 m处发现货车后，立即刹车的同时，不断向前方紧急鸣笛并按闪光灯提醒，货车司机在经过Δt = 1 s后接收到信号，并立即提速，使货车向前做匀加速运动，则其加速度至少多大才能避免相撞？

答案：
(1)设轿车的加速度大小为$a_{1}$，根据运动学公式有$0 - v_{1}^{2}=-2a_{1}x$ (1分)
解得$a_{1}=6$ m/s² (1分)
(2)当两车速度相等时有$v_{2}=v_{1}-a_{1}t_{1}$ (1分)
解得$t_{1}=\frac{10}{3}$ s
此时轿车的位移大小为
$x_{1}=\frac{v_{1}+v_{2}}{2}t_{1}=\frac{200}{3}$ m (1分)
货车匀速运动的位移大小为
$x_{2}=v_{2}t_{1}=\frac{100}{3}$ m (1分)
由于$\Delta x = x_{1}-x_{2}=\frac{100}{3}$ m ＞ $x_{0}=32.5$ m，所以两车会相撞。 (1分)
(3)该路段湿滑后，轿车的加速度大小变为了$a_{1}'=\frac{5}{6}a_{1}=5$ m/s²，设货车的加速度大小为$a_{2}$，$\Delta t$时间内，轿车的位移大小
$x_{1}'=v_{1}\Delta t-\frac{1}{2}a_{1}'(\Delta t)^{2}=27.5$ m (1分)
此时轿车的速度大小
$v = v_{1}'-a_{1}'\Delta t=25$ m/s
货车的位移大小$x_{2}'=v_{2}\Delta t = 10$ m (1分)
此时两车相距$\Delta x'=x_{2}'+x_{0}-x_{1}'=15$ m (1分)
货车司机随后立即加速，设经过$t_{2}$时间后，两车的速度恰好相等。
则有$v_{1}'-a_{1}t_{2}=v_{2}+a_{2}t_{2}$ (1分)
轿车在$t_{2}$时间内匀减速的位移
$x_{3}=v_{1}'t_{2}-\frac{1}{2}a_{1}'t_{2}^{2}$ (1分)
货车在$t_{2}$时间内匀加速的位移
$x_{4}=v_{2}t_{2}+\frac{1}{2}a_{2}t_{2}^{2}$ (1分)
为避免相撞，货车的加速度最小时有
$x_{3}=x_{4}+\Delta x'$ (1分)
联立解得$a_{2}=2.5$ m/s² (1分)