第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
1. 认真读题,细心填空。
(1)大圆半径是小圆半径的2倍,大圆面积是小圆面积的( )倍。
(2)如果一个圆的面积是50.24平方厘米,那么这个圆的半径是( )厘米。
(3)[诊误区]将一个圆平均分成若干份(偶数),拼成一个近似的长方形。已知长方形的长比宽多6.42厘米,则圆的面积是( )平方厘米。
(4)公园里有一个直径为16米的圆形荷花池,在荷花池的周围修一条1米宽的环形石子路,这条石子路的面积是( )平方米,沿这条石子路走一圈,最多走( )米。
(5)从一个正方形中剪一个最大的圆,圆的面积是78.5平方厘米,剩下部分的面积是( )平方厘米。
(6)[推理能力]如图,阴影部分的面积是50平方厘米,则圆环的面积是( )平方厘米。

(1)大圆半径是小圆半径的2倍,大圆面积是小圆面积的( )倍。
(2)如果一个圆的面积是50.24平方厘米,那么这个圆的半径是( )厘米。
(3)[诊误区]将一个圆平均分成若干份(偶数),拼成一个近似的长方形。已知长方形的长比宽多6.42厘米,则圆的面积是( )平方厘米。
(4)公园里有一个直径为16米的圆形荷花池,在荷花池的周围修一条1米宽的环形石子路,这条石子路的面积是( )平方米,沿这条石子路走一圈,最多走( )米。
(5)从一个正方形中剪一个最大的圆,圆的面积是78.5平方厘米,剩下部分的面积是( )平方厘米。
(6)[推理能力]如图,阴影部分的面积是50平方厘米,则圆环的面积是( )平方厘米。

答案:
(1)4
(2)4
(3)28.26 [解析]将一个圆平均分成若干偶数份,拼成一个近似的长方形,长方形的长是$\pi r$,宽是$r$,根据它们的数量关系求出$r$,再求面积。
(4)53.38 56.52 [解析]求石子路的面积就是求圆环的面积,由题可知,内圆直径为16米,环宽为1米,则圆环的面积是3.14×[(16÷2+1)²-(16÷2)²]=53.38(平方米),即这条石子路的面积是53.38平方米;求沿这条石子路走一圈最多走多少米,就是求圆环外圆的周长,外圆的直径是16+1×2=18(米),则外圆的周长是3.14×18=56.52(米),即最多走56.52米。
(5)21.5 [解析]圆的面积是78.5平方厘米,根据圆的面积公式$s = \pi r^2$可得,$r^2 = 78.5÷3.14 = 25$。由图 可知,正方形的边长等于最大的圆的直径,所以正方形的面积是2r×2r=4r²,即正方形的面积是4×25=100(平方厘米),那么剩下部分的面积是100-78.5=21.5(平方厘米)。
可知,正方形的边长等于最大的圆的直径,所以正方形的面积是2r×2r=4r²,即正方形的面积是4×25=100(平方厘米),那么剩下部分的面积是100-78.5=21.5(平方厘米)。
(6)314 [解析]设大圆半径为$R$,小圆半径为$r$。则阴影部分面积为大直角三角形的面积减去小直角三角形的面积,即$(R^2 - r^2)÷2 = 50$,所以$R^2 - r^2 = 100$,则圆环的面积是$\pi(R^2 - r^2)=314$(平方厘米)。
(1)4
(2)4
(3)28.26 [解析]将一个圆平均分成若干偶数份,拼成一个近似的长方形,长方形的长是$\pi r$,宽是$r$,根据它们的数量关系求出$r$,再求面积。
(4)53.38 56.52 [解析]求石子路的面积就是求圆环的面积,由题可知,内圆直径为16米,环宽为1米,则圆环的面积是3.14×[(16÷2+1)²-(16÷2)²]=53.38(平方米),即这条石子路的面积是53.38平方米;求沿这条石子路走一圈最多走多少米,就是求圆环外圆的周长,外圆的直径是16+1×2=18(米),则外圆的周长是3.14×18=56.52(米),即最多走56.52米。
(5)21.5 [解析]圆的面积是78.5平方厘米,根据圆的面积公式$s = \pi r^2$可得,$r^2 = 78.5÷3.14 = 25$。由图
 可知,正方形的边长等于最大的圆的直径,所以正方形的面积是2r×2r=4r²,即正方形的面积是4×25=100(平方厘米),那么剩下部分的面积是100-78.5=21.5(平方厘米)。
可知,正方形的边长等于最大的圆的直径,所以正方形的面积是2r×2r=4r²,即正方形的面积是4×25=100(平方厘米),那么剩下部分的面积是100-78.5=21.5(平方厘米)。(6)314 [解析]设大圆半径为$R$,小圆半径为$r$。则阴影部分面积为大直角三角形的面积减去小直角三角形的面积,即$(R^2 - r^2)÷2 = 50$,所以$R^2 - r^2 = 100$,则圆环的面积是$\pi(R^2 - r^2)=314$(平方厘米)。
2. 反复比较,择优选择。(把正确答案的字母填在括号里)
(1)有两个大小不等的圆,大圆的半径是5厘米,小圆的半径是3厘米,则小圆面积占大圆面积的( )。
A. $\frac{3}{5}$
B. $\frac{3}{25}$
C. $\frac{9}{25}$
D. $\frac{9}{5}$
(2)圆的半径由3厘米增加到7厘米,圆的面积增加了( )。
A. 9平方厘米
B. 40平方厘米
C. 40π平方厘米
D. 16π平方厘米
(3)[几何直观]如图,关于这两个图形中阴影部分的说法正确的是( )。
A. 周长相等,面积不相等
B. 周长、面积都相等
C. 周长不相等,面积相等
D. 无法判断

(1)有两个大小不等的圆,大圆的半径是5厘米,小圆的半径是3厘米,则小圆面积占大圆面积的( )。
A. $\frac{3}{5}$
B. $\frac{3}{25}$
C. $\frac{9}{25}$
D. $\frac{9}{5}$
(2)圆的半径由3厘米增加到7厘米,圆的面积增加了( )。
A. 9平方厘米
B. 40平方厘米
C. 40π平方厘米
D. 16π平方厘米
(3)[几何直观]如图,关于这两个图形中阴影部分的说法正确的是( )。
A. 周长相等,面积不相等
B. 周长、面积都相等
C. 周长不相等,面积相等
D. 无法判断

答案:
(1)C
(2)C
(3)B
(1)C
(2)C
(3)B
3. 求下面阴影部分的面积。


答案:
(1)5×5÷2÷2=6.25(cm²) [解析]如图所示,阴影部分的面积正好等于大直角三角形面积的一半。
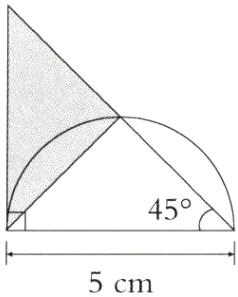
(2)(5+8)×5÷2=32.5(cm²) [解析]如图所示,阴影部分的面积正好等于梯形的面积。

(1)5×5÷2÷2=6.25(cm²) [解析]如图所示,阴影部分的面积正好等于大直角三角形面积的一半。

(2)(5+8)×5÷2=32.5(cm²) [解析]如图所示,阴影部分的面积正好等于梯形的面积。

4. 一个长方形空地的面积是800平方米,宽20米,要在该空地上修一个最大的半圆形喷水池,这个喷水池占地多少平方米?
答案:
800÷20=40(米) 40÷2=20(米)
所以半圆形喷水池的半径为20米。
3.14×20²÷2=628(平方米)
答:这个喷水池占地628平方米。
所以半圆形喷水池的半径为20米。
3.14×20²÷2=628(平方米)
答:这个喷水池占地628平方米。
查看更多完整答案,请扫码查看


