《2025年海淀单元测试AB卷五年级数学下册苏教版》

四明确题意,细心操作。(16分)
1.[新角度]画一画,算一算。(每个小方格的边长为1厘米)(6分)　　　
　　　
(1)在方格图中画一个圆,圆心O的位置是(3,4),圆的半径是2厘米。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　(2)在圆里画一条直径,使直径的一个端点在(x,6)处。　　　　　　　　　　　
　(3)这个圆的面积是(　　　　)平方厘米。　　　　　　　　　　　　　　　　　　

答案：
1.
(1)
(2)题答案如下:
(3)12.56 

2.[新角度]如图是两条互相垂直的直线,相交于O点。

　(1)以〇点为圆心,画一个直径是2厘米的圆。(2分)
　(2)在这个圆内画一个最大的正方形。(2分)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　(3)这个正方形的面积是(　　　　)平方厘米。(1分)
　(4)你画出的这个图形共有(　　　　)条对称轴。(1分)

答案：
2.
(1)
(2)题答案如下: 
(3)2　
(4)4

3.[应用意识]将一个木箱放在桌面上,木箱与桌面的接触面是一个正方形。如图,将一根细绳的一端系在木箱底面的顶点处(O点)。一只爬虫牵着细绳的另一端，从P点按顺时针方向在桌面上爬行,爬行过程中,细绳一直保持拉紧的状态。请你画出爬虫从P点爬到M点的路线。(4分)

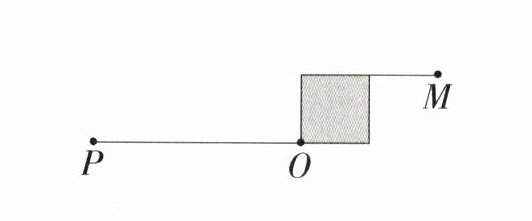
答案：
 3.如下图:

五联系实际,解决问题。(22分)
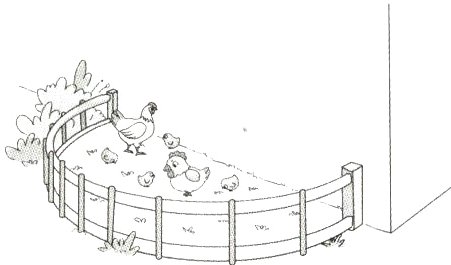
1.张爷爷用25.12米的篱笆靠墙围成一个半圆形的鸡舍，这个鸡舍的占地面积是多少平方米？(3分)
　　

答案： 1.3.14×(25.12×2÷3.14÷2)²÷2 = 100.48(平方米)答:这个鸡舍的占地面积是100.48平方米。

2.给一个缸口是圆形且缸口直径是0.75米的水缸做一个圆形木盖，木盖的直径比缸口的直径长5厘米,木盖的面积是多少平方米？如果沿木盖的外沿钉一圈铁皮,那么铁皮至少长多少厘米?(3分)

答案： 2.5厘米 = 0.05米　(0.75 + 0.05)÷2 = 0.4(米)3.14×0.4² = 0.5024(平方米)3.14×0.4×2 = 2.512(米)　2.512米 = 251.2厘米答:木盖的面积是0.5024平方米，铁皮至少长251.2厘米。

3.(4分)
　

答案： 3.1884÷(3.14×1.5×2×10) = 20(分钟)答:大约需要20分钟。

4.如图，长方形和圆的面积相等，阴影部分的面积是48.96cm²。你能算出圆的面积吗？(5分)
　　　　

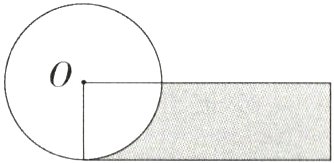
答案： 4.48.96÷3×4 = 65.28(cm²)答:圆的面积是65.28cm²。

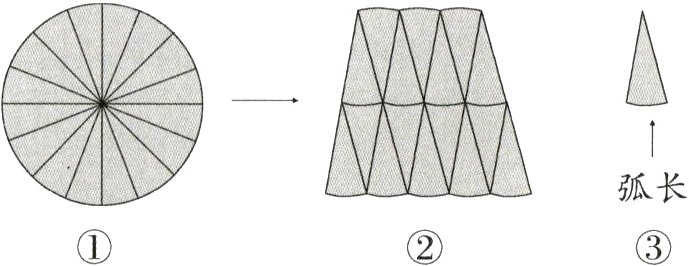
5.[新角度]在学习圆面积公式的推导时,老师带领大家把圆平均分成若干份,再拼成一个近似的长方形，进而推导出圆的面积公式。聪明的小华提出把圆平均分成若干份,再拼成一个近似的梯形(如图,如果分的份数越多，拼成的图形越接近梯形)。你能根据下面的提示，写出他的想法吗？
　(1)如果圆的半径用字母“r"表示，周长用字母“C"表示，把圆平均分成16份后，其中1份(如图③)的弧长相当于圆周长的((　　　　　　　　)),1份中的高相当于圆的(　　　　)。(2分)
　(2)用含有“C"的算式表示梯形(如图②)的上底是(　　　　),下底是(　　　　)。(2分)
(3)利用梯形的面积公式,推导出圆的面积公式,并写出过程。(提示:$\frac{1}{2}$C=πr)(3分)
　　　　　　　　　　　　　　　　　　　　　　

答案： 5.
(1)$\frac{1}{16}$　半径　
(2)$\frac{3}{16}C$　$\frac{5}{16}C$ 
(3)$(\frac{3}{16}C+\frac{5}{16}C)\times2r\div2$=$\frac{1}{2}C\times2r\div2$=$\pi r\times2r\div2$=$2\pi r^{2}\div2$=$\pi r^{2}$[解析]解决此类题型，要联系将圆转化成长方形的经验进行类比思考，找出共同点解决问题。