2025年通成学典课时作业本高中物理选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通成学典课时作业本高中物理选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第45页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
14. (2025·江苏省马坝高级中学期中)一定质
量的理想气体,在等温变化过程中,下列物
理量中没有发生改变的有 (
A.分子的平均动能
B.单位体积内的分子数
C.气体的压强
D.气体的体积
量的理想气体,在等温变化过程中,下列物
理量中没有发生改变的有 (
A
)A.分子的平均动能
B.单位体积内的分子数
C.气体的压强
D.气体的体积
答案:
14. A 解析:等温变化过程中,温度不变,分子的平均动能不变;压强、体积发生相应的变化,则单位体积内的分子数发生变化,选项A正确。
15. (2025·山东济宁期中)汽车胎压监测系统
能够实时监测轮胎气压,系统显示某一轮
胎内的气压为$2.5\mathrm{atm}$,已知该轮胎的容积
为$30\mathrm{L}$,理想气体温度为$0°\mathrm{C}$,阿伏加德罗
常数$N_A = 6.0× 10^{23}\mathrm{mol}^{-1}$,且$0°\mathrm{C}$、$1\mathrm{atm}$
下$1\mathrm{mol}$任何气体的体积均为$22.4\mathrm{L}$,则下
列说法正确的是 (
A.轮胎内每个气体分子的平均距离约为
$2.5× 10^{-9}\mathrm{m}$
B.轮胎内每个气体分子的平均距离约为
$3.5× 10^{-9}\mathrm{m}$
C.该轮胎内气体的分子数约为$1× 10^{24}$个
D.该轮胎内气体的分子数约为$5× 10^{23}$个
能够实时监测轮胎气压,系统显示某一轮
胎内的气压为$2.5\mathrm{atm}$,已知该轮胎的容积
为$30\mathrm{L}$,理想气体温度为$0°\mathrm{C}$,阿伏加德罗
常数$N_A = 6.0× 10^{23}\mathrm{mol}^{-1}$,且$0°\mathrm{C}$、$1\mathrm{atm}$
下$1\mathrm{mol}$任何气体的体积均为$22.4\mathrm{L}$,则下
列说法正确的是 (
A
)A.轮胎内每个气体分子的平均距离约为
$2.5× 10^{-9}\mathrm{m}$
B.轮胎内每个气体分子的平均距离约为
$3.5× 10^{-9}\mathrm{m}$
C.该轮胎内气体的分子数约为$1× 10^{24}$个
D.该轮胎内气体的分子数约为$5× 10^{23}$个
答案:
15. A 解析:由玻意耳定律有$p_0V_0=p_1V_1$,解得$0\ ° C$、$1\ atm$下该轮胎内气体的体积$V_1=75\ L$,则胎内气体分子数$n=\frac{V_1}{22.4\ L}N_A\approx2×10^{24}$,选项CD错误;轮胎内平均每个气体分子所占空间的大小约为$V=\frac{V_0}{n}=\frac{30×10^{-3}}{2×10^{24}}\ m^3=15×10^{-27}\ m^3$,轮胎内每两气体分子之间的距离约为$d=\sqrt[3]{V}\approx2.5×10^{-9}\ m$,选项A正确,B错误。
16. (2025·重庆南开中学期中)为避免潜水员
深潜时出现“氮醉”风险(氮气在高压下易
溶解于血液中,导致潜水员出现类似于醉
酒的症状),需将氮气与氧气在同温、同压
下按体积比为$4:1$混合成“人工空气”供
潜水员使用。如图所示,导热性良好的汽
缸中间有一导热性良好的固定隔板(隔板
上带有关闭的阀门),隔板左右两侧容积相
等,汽缸左侧盛有氧气,右侧盛有氮气(均
视为理想气体)。打开阀门,两气室内气体
混合后恰好满足“人工空气”成分要求,则
混合前左、右气室的压强比为 (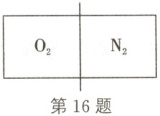
A.$1:4$
B.$4:1$
C.$5:1$
D.$1:5$
深潜时出现“氮醉”风险(氮气在高压下易
溶解于血液中,导致潜水员出现类似于醉
酒的症状),需将氮气与氧气在同温、同压
下按体积比为$4:1$混合成“人工空气”供
潜水员使用。如图所示,导热性良好的汽
缸中间有一导热性良好的固定隔板(隔板
上带有关闭的阀门),隔板左右两侧容积相
等,汽缸左侧盛有氧气,右侧盛有氮气(均
视为理想气体)。打开阀门,两气室内气体
混合后恰好满足“人工空气”成分要求,则
混合前左、右气室的压强比为 (
A
)
A.$1:4$
B.$4:1$
C.$5:1$
D.$1:5$
答案:
16. A 解析:令混合前左、右气室的压强分别为$p_ 左$、$p_ 右$,左、右气室的体积均为$V_0$,混合后氮气与氧气在同温、同压下体积比为$4:1$,令混合后氮气与氧气分别为$4V_1$、$V_1$,对氧气进行分析,根据玻意耳定律有$p_ 右V_0=p_1V_1$,对氮气进行分析,根据玻意耳定律有$p_ 左V_0=p_1·4V_1$,解得$p_ 左:p_ 右=1:4$,选项A正确。
17. 日常生活(2025·山东实验中学模拟)某品
牌“锁鲜包”采用了气调保鲜技术,通过向
包装内充入氮气,隔绝氧气和抑制细菌生
长。如图所示,某锁鲜包容积为$800\mathrm{cm}^3$,包内盛放质量为$250\mathrm{g}$、体积为$200\mathrm{cm}^3$的
辣鸭脖。在$t_1 = -3°\mathrm{C}$的低温车间里封装
完毕后,锁鲜包内气体压强为$p_0$,通过冷链
运输至各销售门店,由于温度改变,锁鲜包
封装膜“鼓起”的体积为锁鲜包容积的$5\%$。
已知销售门店的温度$t_2 = 27°\mathrm{C}$,大气压强
$p_0 = 1× 10^5\mathrm{Pa}$,锁鲜包内外温度始终一致,
求:(锁鲜包内气体视为理想气体,取$T = t + 273\mathrm{K}$)
(1)在门店销售时,锁鲜包内的气体压强$p$
(结果用分数表示)。
(2)为了防止喷溅,在开启包装前,需要先
给锁鲜包“放气”直至包内外压强相同(封
装膜不再鼓起),放气过程中,锁鲜包放出
的气体与封装时包内气体的质量之比。
牌“锁鲜包”采用了气调保鲜技术,通过向
包装内充入氮气,隔绝氧气和抑制细菌生
长。如图所示,某锁鲜包容积为$800\mathrm{cm}^3$,包内盛放质量为$250\mathrm{g}$、体积为$200\mathrm{cm}^3$的
辣鸭脖。在$t_1 = -3°\mathrm{C}$的低温车间里封装
完毕后,锁鲜包内气体压强为$p_0$,通过冷链
运输至各销售门店,由于温度改变,锁鲜包
封装膜“鼓起”的体积为锁鲜包容积的$5\%$。
已知销售门店的温度$t_2 = 27°\mathrm{C}$,大气压强
$p_0 = 1× 10^5\mathrm{Pa}$,锁鲜包内外温度始终一致,
求:(锁鲜包内气体视为理想气体,取$T = t + 273\mathrm{K}$)
(1)在门店销售时,锁鲜包内的气体压强$p$
(结果用分数表示)。
(2)为了防止喷溅,在开启包装前,需要先
给锁鲜包“放气”直至包内外压强相同(封
装膜不再鼓起),放气过程中,锁鲜包放出
的气体与封装时包内气体的质量之比。

答案:
17. 解:
(1)封装时锁鲜包内的气体压强$p_0=1×10^5\ Pa$,体积$V_1=800\ cm^3-200\ cm^3=600\ cm^3$,$T_1=(-3+273) K=270\ K$,在门店销售时,锁鲜包内的气体压强为$p$,$V_2=800\ cm^3×105\%-200\ cm^3=640\ cm^3$,$T_2=(27+273) K=300\ K$,根据理想气体状态方程有$\frac{p_0V_1}{T_1}=\frac{pV_2}{T_2}$,可得$p=\frac{25}{24}×10^5\ Pa$。
(2)设在放气过程中放出的气体体积为$\Delta V$,根据玻意耳定律有$pV_2=p_0(V_1+\Delta V)$,解得$\Delta V=\frac{200}{3}\ cm^3$,则$\frac{\Delta m}{m}=\frac{\Delta V}{V_1+\Delta V}=1:10$。
(1)封装时锁鲜包内的气体压强$p_0=1×10^5\ Pa$,体积$V_1=800\ cm^3-200\ cm^3=600\ cm^3$,$T_1=(-3+273) K=270\ K$,在门店销售时,锁鲜包内的气体压强为$p$,$V_2=800\ cm^3×105\%-200\ cm^3=640\ cm^3$,$T_2=(27+273) K=300\ K$,根据理想气体状态方程有$\frac{p_0V_1}{T_1}=\frac{pV_2}{T_2}$,可得$p=\frac{25}{24}×10^5\ Pa$。
(2)设在放气过程中放出的气体体积为$\Delta V$,根据玻意耳定律有$pV_2=p_0(V_1+\Delta V)$,解得$\Delta V=\frac{200}{3}\ cm^3$,则$\frac{\Delta m}{m}=\frac{\Delta V}{V_1+\Delta V}=1:10$。
查看更多完整答案,请扫码查看


