《2025年通成学典课时作业本高中物理选择性必修第三册人教版》

1.(2025·江西重点高中联考)某氧气瓶的容积为$160 \ {L}$，装满时瓶中气体的压强为$20 \ {atm}$。一机构每天消耗$360 \ {L}$、$1 \ {atm}$的氧气，当氧气瓶中的压强降低到$2 \ {atm}$时，需重新充气。若氧气的温度保持不变，则氧气瓶在该机构循环充气的间隔时间为(气体均视为理想气体)(D)

A.$2$ 天　
B.$4$ 天　
C.$6$ 天　
D.$8$ 天

答案： 1.D 解析：设氧气瓶在该机构循环充气的间隔时间为n
天，根据玻意耳定律有$20p_0×160 L=2p_0×160 L+np_0×360 L$，解得$n=8$，选项D正确。

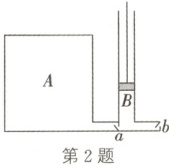
2.(2025·重庆模拟)某同学设计了如图所示装置：$A$为容积为$V$的导热汽缸，通过阀门和细管(容积不计)与最大容积为$0.2V$的导热汽缸$B$相连。$B$内有一厚度不计、可上下运动的活塞，上提活塞时阀门$a$关闭、阀门$b$打开，下压活塞时阀门$b$关闭、阀门$a$打开。外界大气压始终为$p_0$，$A$中空气的初始压强也为$p_0$，活塞每次上、下运动均到达$B$的最高、最低处，整个过程中环境温度保持不变，空气可视为理想气体。活塞从最低处开始先缓慢上提、再缓慢下压计为$1$次，则$5$次后$A$中的气体压强为
(C)


A.$1.2p_0$　
B.$1.4p_0$　
C.$2p_0$　
D.$2.5p_0$

答案： 2.C 解析：5次过程均为充气过程，由$p_0V+p_0×5×0.2V=pV$，可得5次后A中的气体压强$p=2p_0$，选项C
正确。

3.(2025·广东深圳期末)氦气瓶$A$中气体体积为$50 \ {L}$，温度为$17 \degree C$，压强为$760 \ {mmHg}$。现在温度为$162 \degree C$的环境下，通过一个单向压力释放阀对容积为$15 \ {L}$的真空容器$B$供气，当压强差小于$880 \ {mmHg}$时，单向压力释放阀关闭，停止供气。假设供气时不考虑气体的温度变化，气体可视为理想气体。
求：(取$T=t+273 \ {K}$)
(1)开始供气前，$A$内气体的压强。
(2)停止供气时，$B$内气体的压强。

答案： 3.解：
(1)对A中气体分析初态和末态，$p_1=760 mmHg$，
$T_1=290 K$，$T_2=435 K$，供气前A中气体体积不变，由查
理定律有$\frac{p_1}{T_1}=\frac{p_2}{T_2}$，解得$p_2=1140 mmHg$。
(2)停止供气
时，对A中原有气体分析，初态时，$p_2=1140 mmHg$，$V_1=50 L$，末态时，设B容器中压强为$p$，A中气体压强为$p+\Delta p$，$V_1=50 L$，$V=15 L$，由玻意耳定律有$p_2V_1=(p+\Delta p)V_1+pV$，解得$p=200 mmHg$。

4.用活塞式抽气机抽气，在温度不变的情况下，从玻璃瓶中抽气，第一次抽气后，瓶内气体的压强减小到原来的$\frac{4}{5}$，要使容器内剩余气体的压强减为原来的$\frac{256}{625}$，抽气次数应为(气体均视为理想气体)(C)

A.$2$　　
B.$3$　　
C.$4$　　
D.$5$

答案： 4.C 解析：设玻璃瓶的容积是$V$，抽气机的容积是$V_0$，气
体发生等温变化，由玻意耳定律可得$pV=\frac{4}{5}p(V+V_0)$，
解得$V_0=\frac{1}{4}V$，设抽$n$次后，气体压强变为原来的$\frac{256}{625}$，由
玻意耳定律可得：抽一次时$pV=p_1(V+V_0)$，$p_1=\frac{4}{5}p$，抽
两次时$p_1V=p_2(V+V_0)$，$p_2=(\frac{4}{5})^2p$，抽$n$次时$p_n=(\frac{4}{5})^n p$，$p_n=\frac{256}{625}p$，则$n=4$，选项C正确。

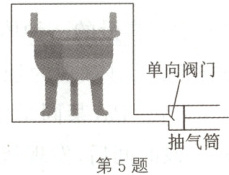
5.为防止文物展出时因氧化而受损，需抽出存放文物的密闭展柜中的空气，充入惰性气体，形成低氧环境。如图所示为用活塞式抽气筒从存放青铜鼎的展柜内抽出空气的示意图。已知展柜的容积为$V_0$，展柜内空气压强为$p_0$，青铜鼎材料的总体积为$\frac{1}{8}V_0$，抽气筒的容积为$\frac{V_0}{16}$。空气视为理想气体，缓慢抽气过程中忽略单向阀门两侧气体的压强差，不考虑抽气引起的温度变化，忽略抽气筒连接管道内气体的体积，求：

(1)将青铜鼎放入展柜后，连接抽气筒，将活塞从单向阀门处向外拉至抽气筒充满气体，此时抽气筒和展柜内气体的总体积。
(2)抽气一次后，展柜内气体的压强。

答案： 5.解：
(1)抽气筒和展柜内气体的总体积$V_1=V_0-\frac{1}{8}V_0+\frac{1}{16}V_0=\frac{15}{16}V_0$。
(2)抽气一次的过程，温度不变，由
玻意耳定律可得$p_0 · (V_0-\frac{1}{8}V_0)=p_1V_1$，解得$p_1=\frac{14}{15}p_0$。