2025年通成学典课时作业本高中物理选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通成学典课时作业本高中物理选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第69页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
8. (2025·河南郑州三模)某实验电路如图所示,交流发电机经过两个理想变压器对负载供电。已知交流发电机输出电压有效值恒定,两变压器间串有电阻$r$,负载为纯电阻。当升压变压器原、副线圈匝数比为$n$时,电阻$r$的功率为$P$,对负载的输电效率为$\eta$;若调节升压变压器原、副线圈匝数比为$0.1n$,则(

A.电阻$r$的功率变为$100P$
B.电阻$r$的功率变为$10P$
C.对负载的输电效率变为$10\eta$
D.对负载的输电效率变为$100\eta$
A
)
A.电阻$r$的功率变为$100P$
B.电阻$r$的功率变为$10P$
C.对负载的输电效率变为$10\eta$
D.对负载的输电效率变为$100\eta$
答案:
8. A 解析:设升压变压器原、副线圈两端的电压分别为$U_{1}$、$U_{2}$,原、副线圈的匝数分别为$n_{1}$、$n_{2}$,则由$\frac{U_{1}}{U_{2}} = \frac{n_{1}}{n_{2}} = n$,解得$U_{2} = \frac{U_{1}}{n}$,设负载电阻为$R$,降压变压器原、副线圈匝数比为$n_{0}$(保持不变);如图所示根据等效电阻法,等效电阻为$n_{0}^{2}R$,则电阻$r$的功率为$P = (\frac{U_{2}}{n_{0}^{2}R + r})^{2} · r = \frac{1}{n^{2}}(\frac{U_{1}}{n_{0}^{2}R + r})^{2} · r$,则当调节升压变压器原、副线圈匝数比为$0.1n$时,电阻$r$的功率变为$100P$,选项A正确,B错误;设通过电阻$r$的电流为$I$,因为是理想变压器,对负载的输电效率为$\eta = \frac{I^{2}n_{0}^{2}R}{I^{2}(n_{0}^{2}R + r)} × 100\% = \frac{n_{0}^{2}R}{n_{0}^{2}R + r} × 100\%$,可得$\eta$保持不变,选项CD错误。

8. A 解析:设升压变压器原、副线圈两端的电压分别为$U_{1}$、$U_{2}$,原、副线圈的匝数分别为$n_{1}$、$n_{2}$,则由$\frac{U_{1}}{U_{2}} = \frac{n_{1}}{n_{2}} = n$,解得$U_{2} = \frac{U_{1}}{n}$,设负载电阻为$R$,降压变压器原、副线圈匝数比为$n_{0}$(保持不变);如图所示根据等效电阻法,等效电阻为$n_{0}^{2}R$,则电阻$r$的功率为$P = (\frac{U_{2}}{n_{0}^{2}R + r})^{2} · r = \frac{1}{n^{2}}(\frac{U_{1}}{n_{0}^{2}R + r})^{2} · r$,则当调节升压变压器原、副线圈匝数比为$0.1n$时,电阻$r$的功率变为$100P$,选项A正确,B错误;设通过电阻$r$的电流为$I$,因为是理想变压器,对负载的输电效率为$\eta = \frac{I^{2}n_{0}^{2}R}{I^{2}(n_{0}^{2}R + r)} × 100\% = \frac{n_{0}^{2}R}{n_{0}^{2}R + r} × 100\%$,可得$\eta$保持不变,选项CD错误。

9. (2025·山东济宁市育才中学段考)(多选)图为通过远距离输电方式给新能源汽车充电桩供电示意图,两变压器均为理想变压器,升压变压器$T_1$和降压变压器$T_2$的原、副线圈匝数比分别为$n_1 : n_2 = 1 : 16$、$n_3 : n_4 = 78 : 5$,输电线总电阻为$r = 2\,\Omega$。在$T_1$的原线圈两端接入一电压为$u = 250 \sqrt{2} \sin(100 \pi t)$V 的交流电。不考虑其他因素的影响,下列说法正确的是
(
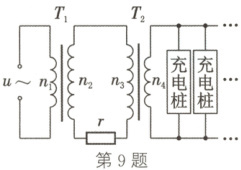
A.充电桩上交流电的周期为 0.01 s
B.当$T_1$的输入功率为 200 kW 时,输电线上损失的电功率为$5 × 10^4$W
C.当$T_1$的输入功率为 200 kW 时,$T_2$的输出电压有效值为 250 V
D.当充电桩使用个数减小时,$T_2$的输出电压增大
(
CD
)
A.充电桩上交流电的周期为 0.01 s
B.当$T_1$的输入功率为 200 kW 时,输电线上损失的电功率为$5 × 10^4$W
C.当$T_1$的输入功率为 200 kW 时,$T_2$的输出电压有效值为 250 V
D.当充电桩使用个数减小时,$T_2$的输出电压增大
答案:
9. CD 解析:充电桩上交流电的周期$T = \frac{2\pi}{\omega} = \frac{2\pi}{100\pi}\ s = 0.02\ s$,选项A错误;当$T_{1}$的输入功率为$200\ kW$时,升压变压器初级电压$U_{1} = \frac{250\sqrt{2}}{\sqrt{2}}\ V = 250\ V$,次级电压$U_{2} = \frac{n_{2}}{n_{1}}U_{1} = 4000\ V$,输电线的电流$I_{2} = \frac{P}{U_{2}} = 50\ A$,输电线上损失的电功率$P_{线} = I_{2}^{2}r = 5 × 10^{3}\ W$,$T_{2}$的输入电压$U_{3} = U_{2} - I_{2}r = 3900\ V$,$T_{2}$的输出电压有效值$U_{4} = \frac{n_{4}}{n_{3}}U_{3} = 250\ V$,选项B错误,C正确;当充电桩使用个数减小时,$T_{2}$的输出功率减小,则输电线的电流减小,输电线损失的电压减小,$T_{2}$的初级电压变大,则$T_{2}$的输出电压增大,选项D正确。
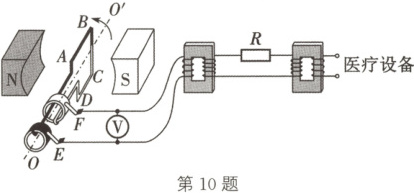
10. 🟦生产生活 (2025·江苏无锡期中)某医院设计的供电系统输电电路简图如图所示,发电机的矩形线框$ABCD$处于磁感应强度大小$B = \frac{\sqrt{2}}{10 \pi} T$的水平匀强磁场中,线框面积$S = 0.25 m^2$,匝数$n = 100$匝,电阻不计。线框绕垂直于磁场的轴$OO'$以一定的角速度匀速转动,并与升压变压器的原线圈相连,升压变压器原、副线圈的匝数之比为 1 : 20,降压变压器的副线圈接入到医院供电,两变压器间的输电线的等效电阻$R = 40\,\Omega$,变压器均为理想变压器。当发电机输出功率$P = 5 × 10^4$W 时,电压表的示数为 250 V,额定电压为 220 V 的医疗设备正常工作。
(1)求线框转动角速度的大小。
(2)求降压变压器原、副线圈匝数之比。
(3)若每台医疗设备的额定功率均为 1 kW,上述情况下,刚好可以满足几台这种同型号的医疗设备同时工作?
(1)求线框转动角速度的大小。
(2)求降压变压器原、副线圈匝数之比。
(3)若每台医疗设备的额定功率均为 1 kW,上述情况下,刚好可以满足几台这种同型号的医疗设备同时工作?

答案:
10. 解:
(1) 电压表示数为有效值,则$U_{1} = \frac{E_{m}}{\sqrt{2}} = 250\ V$,发电机的最大感应电动势$E_{ m} = nBS\omega$,解得线框转动的角速度大小为$\omega = 100\pi\ rad/s$。
(2) 升压变压器副线圈两端电压$U_{2} = \frac{n_{2}}{n_{1}}U_{1} = 5000\ V$,输电线上的电流$I = \frac{P}{U_{2}} = \frac{5 × 10^{4}}{5000}\ A = 10\ A$,降压变压器原线圈两端电压$U_{3} = U_{2} - IR = 4600\ V$,降压变压器原、副线圈匝数之比为$n_{3} : n_{4} = U_{3} : U_{4} = 4600\ V : 220\ V = 230 : 11$。
(3) 医疗设备正常工作的总功率$P_{ 总} = U_{3}I = 4600 × 10\ W = 46\ kW$,所以刚好满足医疗设备同时工作的台数为$x = \frac{46\ kW}{1\ kW} = 46$。
(1) 电压表示数为有效值,则$U_{1} = \frac{E_{m}}{\sqrt{2}} = 250\ V$,发电机的最大感应电动势$E_{ m} = nBS\omega$,解得线框转动的角速度大小为$\omega = 100\pi\ rad/s$。
(2) 升压变压器副线圈两端电压$U_{2} = \frac{n_{2}}{n_{1}}U_{1} = 5000\ V$,输电线上的电流$I = \frac{P}{U_{2}} = \frac{5 × 10^{4}}{5000}\ A = 10\ A$,降压变压器原线圈两端电压$U_{3} = U_{2} - IR = 4600\ V$,降压变压器原、副线圈匝数之比为$n_{3} : n_{4} = U_{3} : U_{4} = 4600\ V : 220\ V = 230 : 11$。
(3) 医疗设备正常工作的总功率$P_{ 总} = U_{3}I = 4600 × 10\ W = 46\ kW$,所以刚好满足医疗设备同时工作的台数为$x = \frac{46\ kW}{1\ kW} = 46$。
查看更多完整答案,请扫码查看


