《2025年通成学典课时作业本高中物理选择性必修第二册人教版》

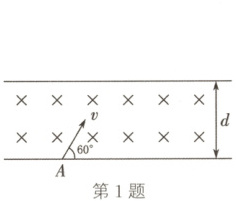
1. (2024·江苏南京期末)如图所示，上下板足够长，间距为$d$。一质量为$m$、电荷量为$+q$的粒子(不计重力)，从下极板上的$A$点以速度$v$沿与极板成$60^{\circ}$角、垂直磁场的方向射入磁场区域。若要使粒子不打在上极板上，则磁场的磁感应强度$B$应满足 (C)

A.$0 ＜ B ＜ \frac{3mv}{2qd}$
B.$0 ＜ B ＜ \frac{mv}{qd}$
C.$B ＞ \frac{3mv}{2qd}$
D.$B ＞ \frac{mv}{qd}$

答案：
1.C　解析:粒子不打在上极板，临界情况为粒子的轨迹恰好与上极板相切，如图所示，设轨道半径为$r$，由几何关系可得$d = r\sin 30^{\circ}+r$，解得$r = \frac{2d}{3}$，由于洛伦兹力提供向心力，则$qvB = m\frac{v^{2}}{r}$，解得$B = \frac{3mv}{2qd}$，磁感应强度$B$越大，轨迹半径越小，所以磁场的磁感应强度$B$应满足$B ＞ \frac{3mv}{2qd}$，选项C正确。

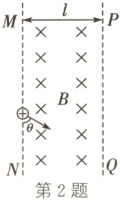
2. (2024·江西抚州期末)如图，真空区域有宽度为$l$、磁感应强度为$B$的匀强磁场，方向如图所示，$MN$、$PQ$是磁场的边界。质量为$m$、电荷量为$q$的带正电粒子(不计重力)沿着与$MN$夹角为$60^{\circ}$的方向射入磁场中，刚好没能从$PQ$边界射出磁场。下列说法正确的是 (C)

A.粒子射入磁场的速度大小为$\frac{4qBl}{3m}$
B.粒子射入磁场的速度大小为$\frac{qBl}{3m}$
C.粒子在磁场中运动的时间为$\frac{4 \pi m}{3qB}$
D.粒子在磁场中运动的时间为$\frac{2 \pi m}{3qB}$

答案：
2.C解析:根据题意可以分析粒子到达$PQ$边界时速度方向与边界线相切，如图所示，则根据几何关系可知$l = r + r\sin 30^{\circ}$，在磁场中做圆周运动，根据洛伦兹力提供向心力有$qvB = m\frac{v^{2}}{r}$，解得$v = \frac{2qBl}{3m}$，选项AB错误；由粒子运动轨迹可知粒子转过的圆心角为$240^{\circ}$，粒子在磁场中运动的周期为$T = \frac{2\pi r}{v} = \frac{2\pi m}{qB}$，则粒子在磁场中运动的时间为$t = \frac{240^{\circ}}{360^{\circ}}T = \frac{4\pi m}{3qB}$，选项C正确，D错误。

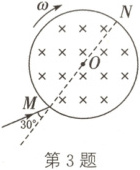
3. (2025·山东泰安期末)一半径为$R$的圆筒处于匀强磁场中，磁场方向与筒的中心轴线平行，筒的横截面如图所示。图中直径$MN$的两端分别开有小孔$M$、$N$，筒绕其中心轴以角速度$\omega$顺时针转动。在该截面内，一带电粒子从小孔$M$射入筒内，射入时的运动方向与$MN$成$30^{\circ}$角。当筒转过$120^{\circ}$时，该粒子恰好从小孔$N$飞出圆筒，不计重力。若粒子在筒内未与筒壁发生碰撞，则带电粒子运动的速度为 (B)

A.$\frac{\sqrt{3} \omega R}{2}$
B.$\frac{\omega R}{2}$
C.$\frac{\sqrt{3} \omega R}{6}$
D.$\frac{\omega R}{6}$

答案：
3.B　解析:粒子恰好从小孔$N$飞出圆筒时筒转过$120^{\circ}$，由几何关系得，粒子在磁场中做匀速圆周运动所转过的圆心角为$60^{\circ}$，半径为$R$，如图所示，则粒子在磁场中做匀速圆周运动的周期$T = 6 × (\frac{1}{3} × \frac{2\pi}{\omega}) = \frac{4\pi}{\omega}$，根据$T = \frac{2\pi m}{qB}$，结合洛伦兹力提供向心力$qvB = m\frac{v^{2}}{R}$，解得$v = \frac{\omega R}{2}$，选项B 正确。

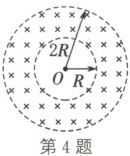
4. (2024·吉林通化期末)如图所示，在以半径为$R$和$2R$的同心圆为边界的区域中，有磁感应强度大小为$B$、方向垂直纸面向里的匀强磁场。在圆心$O$处有一粒子源(图中未画出)，在纸面内沿各个方向发射出比荷为$\frac{q}{m}$的带负电的粒子，粒子的速率分布连续，忽略粒子所受重力和粒子间的相互作用力，已知$\sin 37^{\circ}$取$0.6$，$\cos 37^{\circ}$取$0.8$。若所有的粒子都不能射出磁场，则下列说法正确的是 (C)

A.粒子速度的最大值为$\frac{2qBR}{m}$
B.粒子速度的最大值为$\frac{qBR}{4m}$
C.某粒子恰好不从大圆边界射出磁场，其在磁场中运动的时间为$\frac{127 \pi m}{90qB}$(不考虑粒子再次进入磁场的情况)
D.某粒子恰好不从大圆边界射出磁场，其在磁场中运动的时间为$\frac{4 \pi m}{3qB}$(不考虑粒子再次进入磁场的情况)

答案：
4.C　解析:根据洛伦兹力提供向心力有$qvB = m\frac{v^{2}}{r}$，可得粒子的运动半径$r = \frac{mv}{qB}$，可知粒子速度最大时，运动半径最大，作出粒子的运动轨迹如图所示，根据几何关系有$(2R - r)^{2} = R^{2} + r^{2}$，联立解得$r = \frac{3}{4}R$，$v = \frac{3qBR}{4m}$，选项AB错误；某粒子恰好不从大圆边界射出磁场，即粒子速度最大时，根据几何关系有$\tan\frac{\angle ACD}{2} = \frac{R}{r} = \frac{4}{3}$，可知$\angle ACD = 106^{\circ}$，解得其在磁场中运动的时间$t = \frac{360^{\circ} - \angle ACD}{360^{\circ}} × T = \frac{127\pi m}{90qB}$，选项C正确，D错误。