22. (本小题满分7分)
已知$a$,$b$,$c$为$\triangle ABC$的三边长,且$b$,$c$满足$(b - 2)^2 + |c - 3| = 0$,$a$为方程$|x - 4| = 2$的解.求$\triangle ABC$的周长,并判断$\triangle ABC$的形状.
已知$a$,$b$,$c$为$\triangle ABC$的三边长,且$b$,$c$满足$(b - 2)^2 + |c - 3| = 0$,$a$为方程$|x - 4| = 2$的解.求$\triangle ABC$的周长,并判断$\triangle ABC$的形状.
答案:
因为$(b - 2)^2 + |c - 3| = 0$,且$(b - 2)^2 \geq 0$,$|c - 3| \geq 0$,所以$b - 2 = 0$,$c - 3 = 0$,解得$b = 2$,$c = 3$。
方程$|x - 4| = 2$的解为$x - 4 = 2$或$x - 4 = -2$,即$x = 6$或$x = 2$,所以$a = 6$或$a = 2$。
当$a = 6$时,$b = 2$,$c = 3$,因为$2 + 3 = 5 < 6$,不满足三角形三边关系,舍去;当$a = 2$时,$b = 2$,$c = 3$,满足$2 + 2 > 3$,$2 + 3 > 2$,$2 + 3 > 2$,能构成三角形,故$a = 2$。
$\triangle ABC$的周长为$2 + 2 + 3 = 7$。
因为$a = b = 2$,所以$\triangle ABC$是等腰三角形。
综上,$\triangle ABC$的周长为$7$,是等腰三角形。
方程$|x - 4| = 2$的解为$x - 4 = 2$或$x - 4 = -2$,即$x = 6$或$x = 2$,所以$a = 6$或$a = 2$。
当$a = 6$时,$b = 2$,$c = 3$,因为$2 + 3 = 5 < 6$,不满足三角形三边关系,舍去;当$a = 2$时,$b = 2$,$c = 3$,满足$2 + 2 > 3$,$2 + 3 > 2$,$2 + 3 > 2$,能构成三角形,故$a = 2$。
$\triangle ABC$的周长为$2 + 2 + 3 = 7$。
因为$a = b = 2$,所以$\triangle ABC$是等腰三角形。
综上,$\triangle ABC$的周长为$7$,是等腰三角形。
23. (本小题满分7分)
如图,在$Rt \triangle ABC$中,$\angle ACB = 90^{\circ}$.若$\angle A = 40^{\circ}$,$\triangle ABC$的外角$\angle CBD$的平分线$BE$交$AC$的延长线于点$E$.
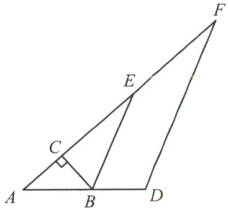
(1)求$\angle CBE$的度数.
(2)过点$D$作$DF // BE$,交$AC$的延长线于点$F$.求$\angle F$的度数.
如图,在$Rt \triangle ABC$中,$\angle ACB = 90^{\circ}$.若$\angle A = 40^{\circ}$,$\triangle ABC$的外角$\angle CBD$的平分线$BE$交$AC$的延长线于点$E$.

(1)求$\angle CBE$的度数.
(2)过点$D$作$DF // BE$,交$AC$的延长线于点$F$.求$\angle F$的度数.
答案:
(1)
在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 40^{\circ}$。
根据直角三角形两锐角互余,可得$\angle ABC=90^{\circ}-\angle A = 90^{\circ}-40^{\circ}=50^{\circ}$。
因为$\angle CBD$是$\triangle ABC$的外角,根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和,所以$\angle CBD=\angle A + \angle ACB=40^{\circ}+90^{\circ}=130^{\circ}$。
因为$BE$平分$\angle CBD$,所以$\angle CBE=\frac{1}{2}\angle CBD=\frac{1}{2}×130^{\circ}=65^{\circ}$。
(2)
因为$\angle ACB = 90^{\circ}$,$\angle CBE = 65^{\circ}$,在$\triangle BCE$中,根据三角形内角和为$180^{\circ}$,可得$\angle CEB=180^{\circ}-\angle ACB - \angle CBE=180^{\circ}-90^{\circ}-65^{\circ}=25^{\circ}$。
因为$DF// BE$,根据两直线平行,同位角相等,所以$\angle F=\angle CEB = 25^{\circ}$。
综上,答案为:
(1)$\angle CBE = 65^{\circ}$;
(2)$\angle F = 25^{\circ}$。
(1)
在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 40^{\circ}$。
根据直角三角形两锐角互余,可得$\angle ABC=90^{\circ}-\angle A = 90^{\circ}-40^{\circ}=50^{\circ}$。
因为$\angle CBD$是$\triangle ABC$的外角,根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和,所以$\angle CBD=\angle A + \angle ACB=40^{\circ}+90^{\circ}=130^{\circ}$。
因为$BE$平分$\angle CBD$,所以$\angle CBE=\frac{1}{2}\angle CBD=\frac{1}{2}×130^{\circ}=65^{\circ}$。
(2)
因为$\angle ACB = 90^{\circ}$,$\angle CBE = 65^{\circ}$,在$\triangle BCE$中,根据三角形内角和为$180^{\circ}$,可得$\angle CEB=180^{\circ}-\angle ACB - \angle CBE=180^{\circ}-90^{\circ}-65^{\circ}=25^{\circ}$。
因为$DF// BE$,根据两直线平行,同位角相等,所以$\angle F=\angle CEB = 25^{\circ}$。
综上,答案为:
(1)$\angle CBE = 65^{\circ}$;
(2)$\angle F = 25^{\circ}$。
查看更多完整答案,请扫码查看


