《2025年云南省标准教辅优佳学案配套测试卷八年级数学上册人教版》

25. (本小题满分8分)
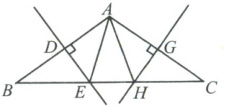
如图，在△ABC中，AB = AC，若DE，GH分别是AB，AC的垂直平分线. 求证：∠BAH = ∠CAE.

答案： 证明：
∵DE是AB的垂直平分线，
∴EA=EB（垂直平分线上的点到线段两端距离相等），
∴∠EAB=∠B（等边对等角）.
∵GH是AC的垂直平分线，
∴HA=HC（垂直平分线上的点到线段两端距离相等），
∴∠HAC=∠C（等边对等角）.
∵AB=AC，
∴∠B=∠C（等边对等角），
∴∠EAB=∠HAC.
∵∠BAH=∠BAC-∠HAC，∠CAE=∠BAC-∠EAB，
∴∠BAH=∠CAE.