《2025年云南省标准教辅优佳学案配套测试卷八年级数学上册人教版》

21. (本小题满分7分)
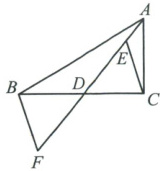
如图，已知AD是△ABC的中线，点E在AD上，连接CE，延长AD至点F，连接BF，使BF//CE. 求证：BF = CE.

答案： 证明：
因为 $AD$ 是 $\triangle ABC$ 的中线，
所以$BD = CD$，
因为 $BF // CE$，
所以$\angle FBD = \angle ECD$，$\angle BFD = \angle CED$，
在 $\triangle BFD$ 和 $\triangle CED$ 中
$\begin{cases}\angle FBD = \angle ECD, \\BD = CD, \\\angle BFD = \angle CED.\end{cases}$
所以 $\triangle BFD \cong \triangle CED (ASA)$，
所以 $BF = CE$。

22. (本小题满分7分)
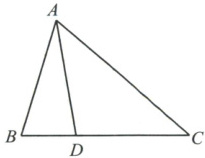
如图，在△ABC中，D是边BC上的一点，连接AD，AB = AD = DC. 若∠BAD = 20°，求∠C的度数.

答案： 设$\angle C=x$，
因为$AD = DC$，
所以$\angle DAC=\angle C=x$，
根据外角性质，$\angle ADB=\angle DAC+\angle C = 2x$，
因为$AB = AD$，
所以$\angle B=\angle ADB = 2x$，
在$\triangle ABD$中，$\angle B + \angle ADB+\angle BAD = 180^{\circ}$，
已知$\angle BAD = 20^{\circ}$，
则$2x+2x + 20^{\circ}=180^{\circ}$，
$4x=160^{\circ}$，
解得$x = 40^{\circ}$，
即$\angle C = 40^{\circ}$。
故答案为：$40^{\circ}$。