20. (本小题满分6分)
如图,已知$\triangle ABC$.
求作:(1)边$AC$上的高.(2)边$BC$上的高.
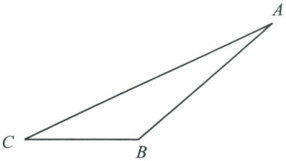
如图,已知$\triangle ABC$.
求作:(1)边$AC$上的高.(2)边$BC$上的高.

答案:
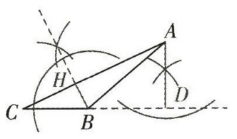

21. (本小题满分6分)
如图,在$\triangle ABC$中,$\angle A = \angle DBC = 36^{\circ}$,$\angle C = 72^{\circ}$.求$\angle 1$,$\angle 2$的度数.
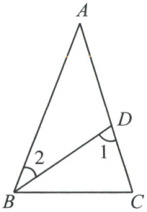
如图,在$\triangle ABC$中,$\angle A = \angle DBC = 36^{\circ}$,$\angle C = 72^{\circ}$.求$\angle 1$,$\angle 2$的度数.

答案:
在$\triangle ABC$中,$\angle A=36^{\circ}$,$\angle C=72^{\circ}$,根据三角形内角和定理,$\angle ABC=180^{\circ}-\angle A-\angle C=180^{\circ}-36^{\circ}-72^{\circ}=72^{\circ}$。
因为$\angle DBC=36^{\circ}$,所以$\angle 2=\angle ABC-\angle DBC=72^{\circ}-36^{\circ}=36^{\circ}$。
在$\triangle DBC$中,$\angle DBC=36^{\circ}$,$\angle C=72^{\circ}$,根据三角形内角和定理,$\angle 1=180^{\circ}-\angle DBC-\angle C=180^{\circ}-36^{\circ}-72^{\circ}=72^{\circ}$。
综上,$\angle 1=72^{\circ}$,$\angle 2=36^{\circ}$。
因为$\angle DBC=36^{\circ}$,所以$\angle 2=\angle ABC-\angle DBC=72^{\circ}-36^{\circ}=36^{\circ}$。
在$\triangle DBC$中,$\angle DBC=36^{\circ}$,$\angle C=72^{\circ}$,根据三角形内角和定理,$\angle 1=180^{\circ}-\angle DBC-\angle C=180^{\circ}-36^{\circ}-72^{\circ}=72^{\circ}$。
综上,$\angle 1=72^{\circ}$,$\angle 2=36^{\circ}$。
查看更多完整答案,请扫码查看


