《2025年云南省标准教辅优佳学案配套测试卷八年级数学上册人教版》

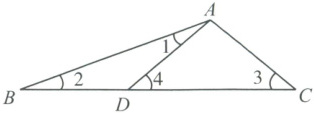
10. 如图，在$\triangle ABC$中，在边$BC$上取一点$D$，使得$\angle 1 = \angle 2 = 20^{\circ}$，$\angle 3 = 2\angle 1$，那么$\angle BAC$的度数为(D).


A.$80^{\circ}$
B.$100^{\circ}$
C.$110^{\circ}$
D.$120^{\circ}$

答案： D

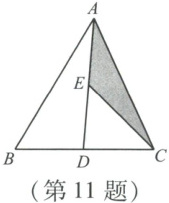
11. 如图，在$\triangle ABC$中，$D$，$E$分别为$BC$，$AD$的中点，且$S_{\triangle ABC} = 4$，则$\triangle AEC$的面积为(B).

A.2
B.1
C.$\frac{1}{2}$
D.$\frac{1}{4}$

答案： B

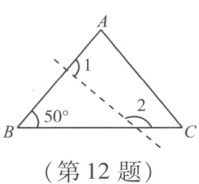
12. 如图，在$\triangle ABC$中，$\angle B = 50^{\circ}$.若沿图中虚线剪去$\angle B$，则$\angle 1 + \angle 2$等于(B).

A.$130^{\circ}$
B.$230^{\circ}$
C.$270^{\circ}$
D.$310^{\circ}$

答案： B

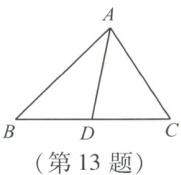
13. 如图，在$\triangle ABC$中，$AB = 8$，$AC = 10$，$D$是边$BC$上的中点，连接$AD$.若$\triangle ACD$的周长为20，则$\triangle ABD$的周长是(A).

A.18
B.22
C.28
D.38

答案： A

14. 下列三角形中，一定为直角三角形的有(C).
①三角形的三边之比为$1:2:3$；
②$\triangle ABC$的三个内角的关系为$\angle A = \frac{1}{2}\angle B = \frac{1}{3}\angle C$；
③三角形的三个内角之比为$4:5:9$；
④三角形的一个外角与它不相邻的两个内角的和为$180^{\circ}$.

A.1个
B.2个
C.3个
D.4个

答案： C

15. 在$\triangle ABC$中，$\angle ABC = \angle C$，$BD$是边$AC$上的高，$\angle ABD = 30^{\circ}$，则$\angle C$的度数为(D).

A.$30^{\circ}$
B.$90^{\circ}$
C.$30^{\circ}$或$90^{\circ}$
D.$30^{\circ}$或$60^{\circ}$

答案： D

16. 已知$\triangle ABC$的两条边长分别为5和8，那么第三条边的长$x$的取值范围是3 ＜ x ＜ 13.

答案： 3 ＜ x ＜ 13

17. 在$\triangle ABC$中，$\angle A + \angle B = 2\angle C$，则$\angle C =$60.

答案： $60^{\circ}$（（题目已经给出角度符号，只填数字即可））。

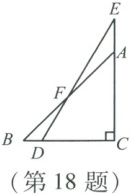
18. 将一副分别含有$30^{\circ}$角和$45^{\circ}$角的两块直角三角尺拼成如图所示的图形，其中$\angle C = 90^{\circ}$，$\angle B = 45^{\circ}$，$\angle E = 30^{\circ}$，则$\angle BFD$的度数是15.

答案： 15

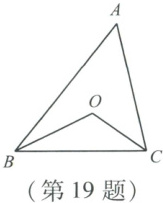
19. 如图，在$\triangle ABC$中，$BO$，$CO$分别平分$\angle ABC$，$\angle ACB$.若$\angle BOC = 110^{\circ}$，则$\angle A =$40.

答案： $40^{\circ}$（填写数值即可，按照题目要求这里可能是填空题，若按给定格式要求这里应填计算结果）