27. (本小题满分10分)
在△ABC中,AB = AC,D是直线BC上一点(不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD = AE,∠DAE = ∠BAC,连接CE.
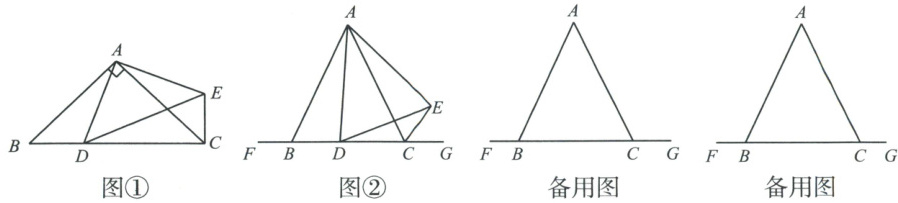
(1)如图①,当点D在线段BC上时,若∠BAC = 90°,则∠BCE =
(2)设∠BAC = α,∠BCE = β.
如图②,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由. 当点D在射线BF和CG上移动时,α,β之间有怎样的数量关系?请直接写出你的结论.
在△ABC中,AB = AC,D是直线BC上一点(不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD = AE,∠DAE = ∠BAC,连接CE.
(1)如图①,当点D在线段BC上时,若∠BAC = 90°,则∠BCE =
90°
.(2)设∠BAC = α,∠BCE = β.
如图②,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由. 当点D在射线BF和CG上移动时,α,β之间有怎样的数量关系?请直接写出你的结论.

答案:
(1)
因为$\angle BAC = \angle DAE$,$\angle BAC=\angle BAD+\angle DAC$,$\angle DAE = \angle EAC+\angle DAC$,
所以$\angle BAD=\angle EAC$。
在$\triangle ABD$和$\triangle ACE$中,$AB = AC$,$\angle BAD=\angle CAE$,$AD = AE$,
根据$SAS$(边角边)定理,可得$\triangle ABD\cong\triangle ACE$。
所以$\angle ABD=\angle ACE$。
因为$AB = AC$,$\angle BAC = 90^{\circ}$,所以$\angle ABC=\angle ACB = 45^{\circ}$。
则$\angle BCE=\angle ACB+\angle ACE=\angle ACB+\\ \angle ABD = 90^{\circ}$。
(2)
当点$D$在线段$BC$上移动时:
因为$\angle BAC=\angle BAD + \angle DAC$,$\angle DAE=\angle CAE+\angle DAC$,且$\angle BAC=\angle DAE$,
所以$\angle BAD=\angle CAE$。
在$\triangle ABD$和$\triangle ACE$中,$AB = AC$,$\angle BAD=\angle CAE$,$AD = AE$,
根据$SAS$定理,$\triangle ABD\cong\triangle ACE$。
所以$\angle ABD=\angle ACE$。
因为$\angle ABD = 180^{\circ}-\alpha-\angle ACB-\angle CAB中的(\angle BAC=\alpha$,且$AB = AC$,$\angle ABC=\angle ACB$,$\angle ABC=\frac{1}{2}(180^{\circ}-\alpha)=90^{\circ}-\frac{\alpha}{2}$,$\angle ABD=\angle ABC$($D$在线段$BC$上)$=\angle ACE$。
$\angle BCE=\angle ACE+\angle ACB$,$\angle ACB = 90^{\circ}-\frac{\alpha}{2}$,$\angle ACE=\angle ABD = 90^{\circ}-\frac{\alpha}{2}$,
所以$\beta=\angle BCE = 180^{\circ}-\alpha$。
当点$D$在射线$BF$上移动时:
同理可证$\triangle ABD\cong\triangle ACE$,$\angle ABD=\angle ACE$。
$\angle ABD = 180^{\circ}-\angle ABC=180^{\circ}-(90^{\circ}-\frac{\alpha}{2})=90^{\circ}+\frac{\alpha}{2}$。
$\angle BCE=\angle ACE-\angle ACB$,$\angle ACE=\angle ABD = 90^{\circ}+\frac{\alpha}{2}$,$\angle ACB = 90^{\circ}-\frac{\alpha}{2}$,
所以$\beta=\angle BCE=\alpha$。
当点$D$在射线$CG$上移动时:
同理可证$\triangle ABD\cong\triangle ACE$,$\angle ABD=\angle ACE$。
$\angle ABD=\angle ABC = 90^{\circ}-\frac{\alpha}{2}$。
$\angle BCE=\angle ACE+\angle ACB$,$\angle ACE=\angle ABD = 90^{\circ}-\frac{\alpha}{2}$,$\angle ACB = 90^{\circ}-\frac{\alpha}{2}$,
所以$\beta=\angle BCE=\alpha$。
综上:
(1)$90^{\circ}$;
(2)当点$D$在线段$BC$上移动时,$\beta = 180^{\circ}-\alpha$;当点$D$在射线$BF$和$CG$上移动时,$\beta=\alpha$。
(1)
因为$\angle BAC = \angle DAE$,$\angle BAC=\angle BAD+\angle DAC$,$\angle DAE = \angle EAC+\angle DAC$,
所以$\angle BAD=\angle EAC$。
在$\triangle ABD$和$\triangle ACE$中,$AB = AC$,$\angle BAD=\angle CAE$,$AD = AE$,
根据$SAS$(边角边)定理,可得$\triangle ABD\cong\triangle ACE$。
所以$\angle ABD=\angle ACE$。
因为$AB = AC$,$\angle BAC = 90^{\circ}$,所以$\angle ABC=\angle ACB = 45^{\circ}$。
则$\angle BCE=\angle ACB+\angle ACE=\angle ACB+\\ \angle ABD = 90^{\circ}$。
(2)
当点$D$在线段$BC$上移动时:
因为$\angle BAC=\angle BAD + \angle DAC$,$\angle DAE=\angle CAE+\angle DAC$,且$\angle BAC=\angle DAE$,
所以$\angle BAD=\angle CAE$。
在$\triangle ABD$和$\triangle ACE$中,$AB = AC$,$\angle BAD=\angle CAE$,$AD = AE$,
根据$SAS$定理,$\triangle ABD\cong\triangle ACE$。
所以$\angle ABD=\angle ACE$。
因为$\angle ABD = 180^{\circ}-\alpha-\angle ACB-\angle CAB中的(\angle BAC=\alpha$,且$AB = AC$,$\angle ABC=\angle ACB$,$\angle ABC=\frac{1}{2}(180^{\circ}-\alpha)=90^{\circ}-\frac{\alpha}{2}$,$\angle ABD=\angle ABC$($D$在线段$BC$上)$=\angle ACE$。
$\angle BCE=\angle ACE+\angle ACB$,$\angle ACB = 90^{\circ}-\frac{\alpha}{2}$,$\angle ACE=\angle ABD = 90^{\circ}-\frac{\alpha}{2}$,
所以$\beta=\angle BCE = 180^{\circ}-\alpha$。
当点$D$在射线$BF$上移动时:
同理可证$\triangle ABD\cong\triangle ACE$,$\angle ABD=\angle ACE$。
$\angle ABD = 180^{\circ}-\angle ABC=180^{\circ}-(90^{\circ}-\frac{\alpha}{2})=90^{\circ}+\frac{\alpha}{2}$。
$\angle BCE=\angle ACE-\angle ACB$,$\angle ACE=\angle ABD = 90^{\circ}+\frac{\alpha}{2}$,$\angle ACB = 90^{\circ}-\frac{\alpha}{2}$,
所以$\beta=\angle BCE=\alpha$。
当点$D$在射线$CG$上移动时:
同理可证$\triangle ABD\cong\triangle ACE$,$\angle ABD=\angle ACE$。
$\angle ABD=\angle ABC = 90^{\circ}-\frac{\alpha}{2}$。
$\angle BCE=\angle ACE+\angle ACB$,$\angle ACE=\angle ABD = 90^{\circ}-\frac{\alpha}{2}$,$\angle ACB = 90^{\circ}-\frac{\alpha}{2}$,
所以$\beta=\angle BCE=\alpha$。
综上:
(1)$90^{\circ}$;
(2)当点$D$在线段$BC$上移动时,$\beta = 180^{\circ}-\alpha$;当点$D$在射线$BF$和$CG$上移动时,$\beta=\alpha$。
查看更多完整答案,请扫码查看


