2025年把关题高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年把关题高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. [成都高二中期]已知函数$y = f(x)(x \in \mathbf{R})$的导函数$f'(x)$的图象如图所示,则函数$y = f(x)($ )
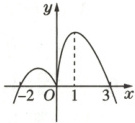
A.在$(-\infty, -2)$上单调递增
B.在$(1, +\infty)$上单调递减
C.在$(-\infty, 3)$上单调递增
D.在$(3, +\infty)$上单调递减

A.在$(-\infty, -2)$上单调递增
B.在$(1, +\infty)$上单调递减
C.在$(-\infty, 3)$上单调递增
D.在$(3, +\infty)$上单调递减
答案:
1.D 解析:由题图可知,当$x < -2$时,$f^{\prime}(x) < 0$,$f(x)$单调递减;当$-2 < x < 3$时,$f^{\prime}(x) \geq 0$且不恒为$0$,$f(x)$单调递增;当$x > 3$时,$f^{\prime}(x) < 0$,$f(x)$单调递减。故选D。
方法总结:解决导数的图象问题,若掌握以下两个常用结论,则能事半功倍。
结论一:正则增,增则正。导数在$x$轴上方的图象所对应的区间为原函数的单调递增区间;反之,若原函数在某个区间上单调递增,则在该区间内导数的图象在$x$轴上方(可与$x$轴有有限个公共点)。
结论二:负则减,减则负。导数在$x$轴下方的图象所对应的区间为原函数的单调递减区间;反之,若原函数在某个区间上单调递减,则在该区间内导数的图象在$x$轴下方(可与$x$轴有有限个公共点)。
方法总结:解决导数的图象问题,若掌握以下两个常用结论,则能事半功倍。
结论一:正则增,增则正。导数在$x$轴上方的图象所对应的区间为原函数的单调递增区间;反之,若原函数在某个区间上单调递增,则在该区间内导数的图象在$x$轴上方(可与$x$轴有有限个公共点)。
结论二:负则减,减则负。导数在$x$轴下方的图象所对应的区间为原函数的单调递减区间;反之,若原函数在某个区间上单调递减,则在该区间内导数的图象在$x$轴下方(可与$x$轴有有限个公共点)。
2. 设$f'(x)$是函数$f(x)$的导函数,将$y = f(x)$的图象和$y = f'(x)$的图象画在同一个平面直角坐标系中,不可能正确的是(
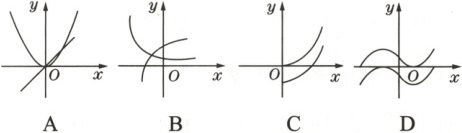
D
)
答案:
2.D 解析:根据原函数单调递增部分对应的导函数图象应在$x$轴上方,而原函数单调递减部分对应的导函数图象应在$x$轴下方可知D不符合。
3. 已知定义域为$\mathbf{R}$的函数$f(x)$的导函数图象如图,则以下函数值的大小关系中,一定正确的是(
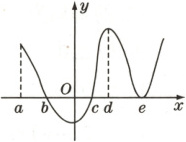
A.$f(a) > f(b) > f(0)$
B.$f(0) < f(c) < f(d)$
C.$f(b) < f(0) < f(c)$
D.$f(c) < f(d) < f(e)$
D
)
A.$f(a) > f(b) > f(0)$
B.$f(0) < f(c) < f(d)$
C.$f(b) < f(0) < f(c)$
D.$f(c) < f(d) < f(e)$
答案:
3.D 解析:由$f(x)$的导函数图象可知,$f(x)$在$(a,b)$,$(c,e)$上单调递增,在$(b,c)$上单调递减,所以$f(a) < f(b)$,A错误;$f(b) > f(0) > f(c)$,B、C错误;$f(c) < f(d) < f(e)$,D正确。
4. [多选题]下列函数中,既是奇函数又在区间$(0,1)$上单调递增的是(
A.$y = 2x^{3} + 4x$
B.$y = x + \sin(-x)$
C.$y = \log_{2}|x|$
D.$y = 2^{x} - 2^{-x}$
ABD
)A.$y = 2x^{3} + 4x$
B.$y = x + \sin(-x)$
C.$y = \log_{2}|x|$
D.$y = 2^{x} - 2^{-x}$
答案:
4.ABD 解析:由奇函数的定义可知,A、B、D均为奇函数,C为偶函数,所以排除C;对于选项A,$y^{\prime}=6x^{2}+4 > 0$,所以$y = 2x^{3}+4x$在$(0,1)$上单调递增;对于选项B,$y^{\prime}=1 - \cos(-x) \geq 0$,且$y^{\prime}$不恒为$0$,所以$y = x + \sin(-x)$在$(0,1)$上单调递增;对于选项D,$y^{\prime}=2^{x}\ln2 + 2^{-x}\ln2 > 0$,所以$y = 2^{x}-2^{-x}$在$(0,1)$上单调递增。故选ABD。
5. [西安中学高二期末]函数$f(x) = \frac{1}{2}x^{2} - \ln x$的单调递减区间为(
A.$(-1,1)$
B.$(-\infty, 1)$
C.$(0,1)$
D.$(1, +\infty)$
C
)A.$(-1,1)$
B.$(-\infty, 1)$
C.$(0,1)$
D.$(1, +\infty)$
答案:
5.C 解析:由题意知,函数$f(x)$的定义域是$(0, +\infty)$,且$f^{\prime}(x)=x - \frac{1}{x}=\frac{(x + 1)(x - 1)}{x}$,所以当$0 < x < 1$时,$f^{\prime}(x) < 0$;当$x > 1$时,$f^{\prime}(x) > 0$,所以其单调递减区间是$(0,1)$。
6. [多选题]下列函数是增函数的有(
A.$y = x^{3} + x$
B.$y = \sqrt{x} + \log_{2}x$
C.$y = x\ln x$
D.$y = \ln(x - 1) + (x - 1)^{2}$
ABD
)A.$y = x^{3} + x$
B.$y = \sqrt{x} + \log_{2}x$
C.$y = x\ln x$
D.$y = \ln(x - 1) + (x - 1)^{2}$
答案:
6.ABD 解析:对于A,$y = x^{3}+x$的定义域为$\mathbf{R}$,且$y^{\prime}=3x^{2}+1 \geq 1$,故该函数在其定义域内是增函数,故A符合题意;对于B,$y = \sqrt{x}+\log_{2}x$的定义域为$(0, +\infty)$,且$y^{\prime}=\frac{1}{2}x^{-\frac{1}{2}}+\frac{1}{x\ln2} > 0$,故该函数在其定义域内是增函数,故B符合题意;对于C,$y = x\ln x$的定义域为$(0, +\infty)$,且$y^{\prime}=\ln x + 1$,当$0 < x < \frac{1}{e}$时,$y^{\prime}< 0$,当$x > \frac{1}{e}$时,$y^{\prime}> 0$,所以该函数在$(0,\frac{1}{e})$上单调递减,在$(\frac{1}{e}, +\infty)$上单调递增,故该函数不是增函数,故C不符合题意;对于D,$y = \ln(x - 1)+(x - 1)^{2}$的定义域为$(1, +\infty)$,且$y^{\prime}=\frac{1}{x - 1}+2(x - 1) > 0$,所以该函数在其定义域内是增函数,故D符合题意。
7. [多选题] [2023青岛高二期末]已知函数$f(x) = e^{x} - \cos^{2}x$,则下列结论正确的有(
A.$f(x)$在$\left(0, \frac{\pi}{2}\right)$上单调递增
B.$f(x)$在$\left(0, \frac{\pi}{2}\right)$上单调递减
C.$\forall x \geq 0, f(x) \geq 0$
D.$\exists x_{0} < 0, f(x_{0}) < 0$
ACD
)A.$f(x)$在$\left(0, \frac{\pi}{2}\right)$上单调递增
B.$f(x)$在$\left(0, \frac{\pi}{2}\right)$上单调递减
C.$\forall x \geq 0, f(x) \geq 0$
D.$\exists x_{0} < 0, f(x_{0}) < 0$
答案:
7.ACD 解析:$f^{\prime}(x)=e^{x}+2\cos x·\sin x = e^{x}+\sin2x$,当$x\in(0,\frac{\pi}{2})$时,$\sin2x > 0$,$e^{x} > 0$,$\therefore f^{\prime}(x) > 0$,$\therefore f(x)$在$(0,\frac{\pi}{2})$上单调递增,故A正确,B错误;$\therefore$当$x\in[0,\frac{\pi}{2})$时,$f(x)\geq f(0)=0$①;当$x\geq\frac{\pi}{2}$时,$f(x)=e^{x}-\cos^{2}x - 1 > e - 1$恒成立②,由①②得$\forall x\geq0$,$f(x)\geq0$,故C正确。当$x = -\pi$时,$e^{-\pi}-\cos^{2}\pi < 0$,故D正确。
利用导数判断函数$y = f(x)$的单调性步骤:第1步确定函数的定义域;第2步求出导数$f^{\prime}(x)$的零点;第3步用$f^{\prime}(x)$的零点将$f(x)$的定义域划分为若干个区间,确定$f^{\prime}(x)$在各区间上的正负,由此得出函数$y = f(x)$在定义域内的单调性。【注意】也可通过:求函数定义域$\to$解不等式$f^{\prime}(x)>0(<0)\to$下结论,这三个步骤求解。
利用导数判断函数$y = f(x)$的单调性步骤:第1步确定函数的定义域;第2步求出导数$f^{\prime}(x)$的零点;第3步用$f^{\prime}(x)$的零点将$f(x)$的定义域划分为若干个区间,确定$f^{\prime}(x)$在各区间上的正负,由此得出函数$y = f(x)$在定义域内的单调性。【注意】也可通过:求函数定义域$\to$解不等式$f^{\prime}(x)>0(<0)\to$下结论,这三个步骤求解。
8. [2024贵阳高二期末]已知函数$f(x) = (2 - a)x - \ln x - 1$. 当$a > 0$时,设$g(x) = f(x) + ax^{2}$,求函数$g(x)$的单调区间.
答案:
8.解:$g(x)=ax^{2}+(2 - a)x - \ln x - 1$,其定义域为$(0, +\infty)$,$\therefore g^{\prime}(x)=2ax + 2 - a - \frac{1}{x}=\frac{2ax^{2}+(2 - a)x - 1}{x}=\frac{(2x - 1)(ax + 1)}{x}$。$\because a > 0$,$\therefore ax + 1 > 0$,$\therefore$当$x\in[\frac{1}{2}, +\infty)$时,$g^{\prime}(x) > 0$;当$x\in(0,\frac{1}{2})$时,$g^{\prime}(x) < 0$,$\therefore g(x)$的单调递增区间为$[\frac{1}{2}, +\infty)$,单调递减区间为$(0,\frac{1}{2})$。
查看更多完整答案,请扫码查看


