2025年小题狂做高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 若函数 $ g(x)=\mathrm{e}^{x} f(x)(\mathrm{e} \approx 2.71828 $ 是自然对数的底数)在 $ f(x) $ 的定义域上单调递减,则称函数 $ f(x) $ 具有 $ N $ 性质.下列函数具有 $ N $ 性质的为( )
A.$ f(x)=3^{-x} $
B.$ f(x)=x $
C.$ f(x)=x^{2}+1 $
D.$ f(x)=-x^{2}-3 $
A.$ f(x)=3^{-x} $
B.$ f(x)=x $
C.$ f(x)=x^{2}+1 $
D.$ f(x)=-x^{2}-3 $
答案:
8. AD 对于A,$f(x) = 3^{-x}$,则$g(x) = 3^{-x} · \mathrm{e}^{x} = (\frac{\mathrm{e}}{3})^{x}$,
又因为$0 < \frac{\mathrm{e}}{3} < 1$,所以$g(x)$在$\mathbf{R}$上单调递减,即$f(x)$具有
N性质,故A符合;对于B,$f(x) = x$,则$g(x) = x\mathrm{e}^{x}$,所
以$g^{\prime}(x) = \mathrm{e}^{x}(x + 1)$,令$g^{\prime}(x) > 0$,解得$x > -1$,令
$g^{\prime}(x) < 0$,解得$x < -1$,所以$g(x)$在$(-\infty, -1)$上单调递
减,在$(-1, +\infty)$上单调递增,所以$g(x)$在$\mathbf{R}$上不单调,即
$f(x)$不具有N性质,故B不符合;对于C,$f(x) = x^{2} + 1$,
则$g(x) = \mathrm{e}^{x}(x^{2} + 1)$,所以$g^{\prime}(x) = \mathrm{e}^{x}(x^{2} + 1 + 2x) =\mathrm{e}^{x}(x + 1)^{2} \geqslant 0$,所以$g(x)$在$\mathbf{R}$上单调递增,即$f(x)$不具有
N性质,故C不符合;对于D,$f(x) = -x^{2} - 3$,则$g(x) =\mathrm{e}^{x}(-x^{2} - 3)$,所以$g^{\prime}(x) = \mathrm{e}^{x}(-x^{2} - 3 - 2x) = -\mathrm{e}^{x}[(x + 1)^{2} + 2] < 0$,所以$g(x)$在$\mathbf{R}$上单调递
减,即$f(x)$具有N性质,故D符合.
又因为$0 < \frac{\mathrm{e}}{3} < 1$,所以$g(x)$在$\mathbf{R}$上单调递减,即$f(x)$具有
N性质,故A符合;对于B,$f(x) = x$,则$g(x) = x\mathrm{e}^{x}$,所
以$g^{\prime}(x) = \mathrm{e}^{x}(x + 1)$,令$g^{\prime}(x) > 0$,解得$x > -1$,令
$g^{\prime}(x) < 0$,解得$x < -1$,所以$g(x)$在$(-\infty, -1)$上单调递
减,在$(-1, +\infty)$上单调递增,所以$g(x)$在$\mathbf{R}$上不单调,即
$f(x)$不具有N性质,故B不符合;对于C,$f(x) = x^{2} + 1$,
则$g(x) = \mathrm{e}^{x}(x^{2} + 1)$,所以$g^{\prime}(x) = \mathrm{e}^{x}(x^{2} + 1 + 2x) =\mathrm{e}^{x}(x + 1)^{2} \geqslant 0$,所以$g(x)$在$\mathbf{R}$上单调递增,即$f(x)$不具有
N性质,故C不符合;对于D,$f(x) = -x^{2} - 3$,则$g(x) =\mathrm{e}^{x}(-x^{2} - 3)$,所以$g^{\prime}(x) = \mathrm{e}^{x}(-x^{2} - 3 - 2x) = -\mathrm{e}^{x}[(x + 1)^{2} + 2] < 0$,所以$g(x)$在$\mathbf{R}$上单调递
减,即$f(x)$具有N性质,故D符合.
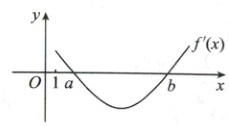
9. 已知三次函数 $ f(x) $ 的导函数 $ f'(x) $ 的图象如图所示,且 $ f(m)=f(k)=f(t)=1,m < k < t $,则( )
A.$ m + k < a + b < t + k $
B.$ f(b) < 1 < f(a) $
C.$ f'(m) · f'(k) · f'(t) < 0 $
D.$ f'(a^{2} b) > f'(k t a) $

A.$ m + k < a + b < t + k $
B.$ f(b) < 1 < f(a) $
C.$ f'(m) · f'(k) · f'(t) < 0 $
D.$ f'(a^{2} b) > f'(k t a) $
答案:
9. ABC 根据导函数$f^{\prime}(x)$的图象,可知$f^{\prime}(a) = 0$,
$f^{\prime}(b) = 0$,当$x < a$时,$f^{\prime}(x) > 0$,当$a < x < b$时,$f^{\prime}(x) <0$,当$x > b$时,$f^{\prime}(x) > 0$,所以$f(x)$在$(-\infty, a)$上单调递
增,在$(a, b)$上单调递减,在$(b, +\infty)$上单调递增,故其大致
图象如图所示,则有$m < a < k < b < t$,故A正确;又$f(b) < 1 < f(a)$,故B正确;结合$m <a < k < b < t$,得$f^{\prime}(m) > 0$,$f^{\prime}(k) < 0$,$f^{\prime}(t) > 0$,所以
$f^{\prime}(m) · f^{\prime}(k) · f^{\prime}(t) < 0$,故C正确;因为$1 < a < k < b <t$,所以$1 < ab < kt$,$b < a^{2}b < kta$,又$f^{\prime}(x)$在$(b, +\infty)$上单调
递增,故$f^{\prime}(a^{2}b) < f^{\prime}(kta)$,故D错误.
$f^{\prime}(b) = 0$,当$x < a$时,$f^{\prime}(x) > 0$,当$a < x < b$时,$f^{\prime}(x) <0$,当$x > b$时,$f^{\prime}(x) > 0$,所以$f(x)$在$(-\infty, a)$上单调递
增,在$(a, b)$上单调递减,在$(b, +\infty)$上单调递增,故其大致
图象如图所示,则有$m < a < k < b < t$,故A正确;又$f(b) < 1 < f(a)$,故B正确;结合$m <a < k < b < t$,得$f^{\prime}(m) > 0$,$f^{\prime}(k) < 0$,$f^{\prime}(t) > 0$,所以
$f^{\prime}(m) · f^{\prime}(k) · f^{\prime}(t) < 0$,故C正确;因为$1 < a < k < b <t$,所以$1 < ab < kt$,$b < a^{2}b < kta$,又$f^{\prime}(x)$在$(b, +\infty)$上单调
递增,故$f^{\prime}(a^{2}b) < f^{\prime}(kta)$,故D错误.
10. 若函数 $ f(x)=-\frac{1}{3} x^{3}+a x $ 有三个单调区间,则实数 $ a $ 的取值范围是____.
答案:
10. $(0, +\infty)$ $f^{\prime}(x) = -x^{2} + a$,由于函数$f(x)$有三个单调区间,所以$f^{\prime}(x) = -x^{2} + a = 0$有两个不相等的实数根,即$a > 0$.
11. (易错易混)函数 $ f(x)=\ln x-\frac{x + 1}{x - 1} $ 的单调递增区间为____.
答案:
11. $(0, 1)$和$(1, +\infty)$ 定义域为$(0, 1) \cup (1, +\infty)$,
$f^{\prime}(x) = \frac{1}{x} - \frac{x - 1 - (x + 1)}{(x - 1)^{2}} = \frac{1}{x} - \frac{-2}{(x - 1)^{2}} = \frac{x^{2} + 1}{x(x - 1)^{2}}$.
由$f^{\prime}(x) = \frac{x^{2} + 1}{x(x - 1)^{2}} > 0$,再结合函数的定义域可得$0 <x < 1$或$x > 1$,所以函数$f(x)$的单调递增区间为$(0, 1)$和
$(1, +\infty)$.
$f^{\prime}(x) = \frac{1}{x} - \frac{x - 1 - (x + 1)}{(x - 1)^{2}} = \frac{1}{x} - \frac{-2}{(x - 1)^{2}} = \frac{x^{2} + 1}{x(x - 1)^{2}}$.
由$f^{\prime}(x) = \frac{x^{2} + 1}{x(x - 1)^{2}} > 0$,再结合函数的定义域可得$0 <x < 1$或$x > 1$,所以函数$f(x)$的单调递增区间为$(0, 1)$和
$(1, +\infty)$.
12. 已知函数 $ y = f(x)(x \in \mathbf{R}) $ 上任一点 $ (x_{0},f(x_{0})) $ 处的切线斜率 $ k=(x_{0}-2)(x_{0}+1)^{2} $,则该函数的单调递减区间为____.
答案:
12. $(-\infty, 2]$ 令$k \leq 0$,得$x_{0} \leq 2$.
13. (教材变式)利用导数判断下列函数的单调性.
(1) $ f(x)=(x^{2}+1) \mathrm{e}^{x} $;
(2) $ f(x)=x \sin x+\cos x(0 < x < \pi) $.
(1) $ f(x)=(x^{2}+1) \mathrm{e}^{x} $;
(2) $ f(x)=x \sin x+\cos x(0 < x < \pi) $.
答案:
13. 解:
(1)因为$f^{\prime}(x) = (x^{2} + 2x + 1)\mathrm{e}^{x} = (x + 1)^{2}\mathrm{e}^{x} \geqslant 0$,
所以$f(x)$在$\mathbf{R}$上单调递增.
(2)因为$f^{\prime}(x) = \sin x + x\cos x - \sin x = x\cos x$,所以当
$x \in (0, \frac{\pi}{2})$时,$f^{\prime}(x) > 0$,$f(x)$单调递增;当$x \in (\frac{\pi}{2}, \pi)$
时,$f^{\prime}(x) < 0$,$f(x)$单调递减.所以$f(x)$在$(0, \frac{\pi}{2})$上单调
递增,在$(\frac{\pi}{2}, \pi)$上单调递减.
(1)因为$f^{\prime}(x) = (x^{2} + 2x + 1)\mathrm{e}^{x} = (x + 1)^{2}\mathrm{e}^{x} \geqslant 0$,
所以$f(x)$在$\mathbf{R}$上单调递增.
(2)因为$f^{\prime}(x) = \sin x + x\cos x - \sin x = x\cos x$,所以当
$x \in (0, \frac{\pi}{2})$时,$f^{\prime}(x) > 0$,$f(x)$单调递增;当$x \in (\frac{\pi}{2}, \pi)$
时,$f^{\prime}(x) < 0$,$f(x)$单调递减.所以$f(x)$在$(0, \frac{\pi}{2})$上单调
递增,在$(\frac{\pi}{2}, \pi)$上单调递减.
14. 求函数 $ f(x)=(1 - a) \ln x+x+\frac{a}{x}-2(a \in \mathbf{R}) $ 的单调区间.
答案:
14. 解:因为$f^{\prime}(x) = \frac{1 - a}{x} + 1 - \frac{a}{x^{2}} = \frac{x^{2} + (1 - a)x - a}{x^{2}} =\frac{(x + 1)(x - a)}{x^{2}}(x > 0)$,所以当$a \leq 0$时,$f^{\prime}(x) > 0$,故函数
$f(x)$在$(0, +\infty)$上单调递增.当$a > 0$时,令$f^{\prime}(x) > 0$,得$x > a$;令$f^{\prime}(x) < 0$,得$0 < x < a$.故函数$f(x)$在$(0, a)$上单调递减,在$(a, +\infty)$上单调递增.综上所述,当$a \leq 0$时,函数$f(x)$的单调递增区间为$(0, +\infty)$,无单调递减区间;当$a > 0$时,函数$f(x)$的单调递增区间为$(a, +\infty)$,单调递减区间为$(0, a)$.
$f(x)$在$(0, +\infty)$上单调递增.当$a > 0$时,令$f^{\prime}(x) > 0$,得$x > a$;令$f^{\prime}(x) < 0$,得$0 < x < a$.故函数$f(x)$在$(0, a)$上单调递减,在$(a, +\infty)$上单调递增.综上所述,当$a \leq 0$时,函数$f(x)$的单调递增区间为$(0, +\infty)$,无单调递减区间;当$a > 0$时,函数$f(x)$的单调递增区间为$(a, +\infty)$,单调递减区间为$(0, a)$.
查看更多完整答案,请扫码查看


