《2025年小题狂做高中数学选择性必修第二册人教版》

1. 设函数 $ f(x) $ 在 $ x = x_0 $ 附近有定义，且有 $ f(x_0 + \Delta x) - f(x_0) = a\Delta x + b(\Delta x)^2 $，其中 $ a $，$ b $ 为常数，则 （ ）

A.$ f'(x) = a $
B.$ f'(x) = b $
C.$ f'(x_0) = a $
D.$ f'(x_0) = b $

答案： 1. C 由题意得$\frac {f(x_0 + \Delta x) - f(x_0)} {\Delta x} = a + b\Delta x$，则$\lim_{\Delta x \to 0} \frac {f(x_0 + \Delta x) - f(x_0)} {\Delta x} = \lim_{\Delta x \to 0} (a + b\Delta x) = a$，即$f'(x_0) = a$.

2. 若函数 $ f(x) $ 在 $ x = x_0 $ 处可导，则 $ \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} $ （ ）

A.与 $ x_0 $，$ h $ 都有关
B.仅与 $ x_0 $ 有关，而与 $ h $ 无关
C.仅与 $ h $ 有关，而与 $ x_0 $ 无关
D.与 $ x_0 $，$ h $ 均无关

答案： 2. B $\lim_{h \to 0} \frac {f(x_0 + h) - f(x_0)} {h} = \lim_{h \to 0} \frac {f(x_0 + h) - f(x_0)} {(x_0 + h) - x_0}=f'(x_0)$，与$x_0$有关，与$h$无关.

3. （易错易混）若 $ \lim_{\Delta x \to 0} \frac{f(x_0 + 3\Delta x) - f(x_0)}{\Delta x} = 1 $，则 $ f'(x_0) = $ （ ）

A.1
B.0
C.3
D.$ \frac{1}{3} $

答案： 3. D 由条件知$\lim_{\Delta x \to 0} \frac {f(x_0 + 3\Delta x) - f(x_0)} {\Delta x} = 1$，所以$\lim_{\Delta x \to 0} \frac {f(x_0 + \Delta x) - f(x_0)} {\Delta x} = \frac {1} {3}$，所以$f'(x_0) = \frac {1} {3}$.

4. （教材变式）函数 $ f(x) = \frac{1}{2x} $ 在 $ x = 2 $ 处的导数为 （ ）

A.2
B.$ \frac{1}{2} $
C.$ \frac{1}{4} $
D.$ -\frac{1}{8} $

答案： 4. D $\lim_{\Delta x \to 0} \frac {\Delta f(x)} {\Delta x} = \lim_{\Delta x \to 0} \frac {f(2 + \Delta x) - f(2)} {\Delta x} = \lim_{\Delta x \to 0} \frac{\frac{1}{2(2 + \Delta x)} - \frac{1}{2×2}}{\Delta x} = \lim_{\Delta x \to 0} (-\frac{1}{2} · \frac{1}{4 + 2\Delta x}) = - \frac {1} {8}$，所以函数$f(x)$在$x = 2$处的导数为$- \frac {1} {8}$.
教材链接人教A版选择性必修二5.1.2例1

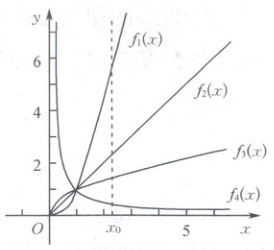
5. 已知函数 $ f_1(x) $，$ f_2(x) $，$ f_3(x) $，$ f_4(x) $，它们在平面直角坐标系中的图象如图所示，则 $ f_1'(x_0) $，$ f_2'(x_0) $，$ f_3'(x_0) $，$ f_4'(x_0) $ 的大小关系是 （ ）

A.$ f_1'(x_0) ＞ f_2'(x_0) ＞ f_3'(x_0) ＞ f_4'(x_0) $
B.$ f_1'(x_0) ＞ f_3'(x_0) ＞ f_2'(x_0) ＞ f_4'(x_0) $
C.$ f_4'(x_0) ＞ f_1'(x_0) ＞ f_3'(x_0) ＞ f_2'(x_0) $
D.$ f_3'(x_0) ＞ f_1'(x_0) ＞ f_4'(x_0) ＞ f_2'(x_0) $

答案： 5. A 依次作出$f_1(x),f_2(x),f_3(x),f_4(x)$在$x = x_0$处的切线，如图，根据图象中切线的斜率可知$f_1'(x_0) ＞ f_2'(x_0) ＞ f_3'(x_0) ＞ f_4'(x_0)$.

6. 已知函数 $ y = f(x) $ 的图象在点 $ P(5, f(5)) $ 处的切线方程是 $ y = -x + 8 $，则 $ f(5) + f'(5) = $ （ ）

A.2
B.3
C.4
D.5

答案： 6. A 易得切点$P(5,3)$，所以$f(5) = 3,k = -1$，即$f'(5) = -1$.所以$f(5) + f'(5) = 3 - 1 = 2$.

7. 已知函数 $ y = f(x) $，下列说法正确的是 （ ）

A.$ \Delta y = f(x_0 + \Delta x) - f(x_0) $ 叫作函数值的增量
B.$ \frac{\Delta y}{\Delta x} = \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} $ 叫作函数从 $ x_0 $ 到 $ x_0 + \Delta x $ 的平均变化率
C.$ f(x) $ 在 $ x = x_0 $ 处的导数记为 $ y' $
D.$ f(x) $ 在 $ x = x_0 $ 处的导数记为 $ f'(x_0) $

答案： 7. ABD $\Delta y = f(x_0 + \Delta x) - f(x_0)$叫作函数值的改变量，即函数值的增量，故A正确；$\frac{\Delta y}{\Delta x} = \frac {f(x_0 + \Delta x) - f(x_0)} {\Delta x}$称为函数$f(x)$从$x_0$到$x_0 + \Delta x$的平均变化率，故B正确；由导数的定义知函数$f(x)$在$x = x_0$处的导数记为$f'(x_0)$，故C错误，D正确.

8. 下列结论正确的是 （ ）

A.函数 $ y = x^3 - 2x $ 在 $ x = -1 $ 处的导数为 1
B.一个做直线运动的物体从时间 $ t $ 到 $ t + \Delta t $ 的位移为 $ \Delta s $，那么 $ \lim_{\Delta t \to 0} \frac{\Delta s}{\Delta t} $ 表示 $ t $ 时刻该物体的瞬时速度
C.当物体做直线运动时，它的运动规律可以用函数 $ v = v(t) $ 表示，其中 $ v $ 表示瞬时速度，$ t $ 表示时间，则该物体在 $ t $ 时刻的加速度为 $ \lim_{\Delta t \to 0} \frac{v(t + \Delta t) - v(t)}{\Delta t} $
D.函数 $ f(x) $ 在 $ x = x_0 $ 处的导数 $ f'(x_0) $ 的几何意义是点 $ (x_0, f(x_0)) $ 与点 $ (0, 0) $ 连线的斜率

答案： 8. ABC $y'\big|_{x = -1} = \lim_{\Delta x \to 0} \frac {(-1 + \Delta x)^3 - 2(-1 + \Delta x) - (-1)^3 + 2 × (-1)} {\Delta x} = \lim_{\Delta x \to 0} [(\Delta x)^2 - 3\Delta x + 1] = 1$，故A正确；根据平均变化率和瞬时速度的概念可知，一个做直线运动的物体从时间$t$到$t + \Delta t$的位移为$\Delta s$，那么$\lim_{\Delta t \to 0} \frac {\Delta s} {\Delta t}$表示在$t$时刻该物体的瞬时速度，故B正确；根据平均变化率和瞬时速度的概念可知，当物体做直线运动时，它的运动规律可以用函数$v = v(t)$表示，其中$v$表示瞬时速度，$t$表示时间，则该物体在$t$时刻的加速度为$\lim_{\Delta t \to 0} \frac {v(t + \Delta t) - v(t)} {\Delta t}$，故C正确；$f'(x_0)$的几何意义是$f(x)$在$x = x_0$处的切线的斜率，故D错误.