2025年小题狂做高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 在等差数列$ \{ a_{n}\} $中,$ S_{2}=2 $,$ S_{3}=-6 $,则 $ a_{n}= $____.
答案:
10. $-6n+10$ $a_3=S_3-S_2=-6-2=-8$,即$a_1+2d=-8$.又$S_2=2a_1+d=2$,解得$a_1=4,d=-6$.所以$a_n=4-6(n-1)=-6n+10$.
11. 已知 $ S_{n} $ 是等差数列$ \{ a_{n}\} $的前 $ n $ 项和. 若$ \frac{a_{5}}{a_{3}}=\frac{10}{9} $,则$ \frac{S_{9}}{S_{5}} $的值是____.
答案:
11. 2 $\frac{\frac{1}{2}(a_1+a_9) × 9}{\frac{1}{2}(a_1+a_5) × 5}=\frac{9a_5}{5a_3}=\frac{9}{5} × \frac{10}{9}=2$.
12. (教材变式)在等差数列$ \{ a_{n}\} $中,奇数项之和为 220,偶数项之和为 165,若此数列的项数为 10,则此数列的公差为____;若此数列的项数为奇数,则此数列的中间项是____.
答案:
12. $-11$ $55$ 设数列$\{a_n\}$的公差为$d$.若此数列的项数为偶数,设项数为$2n,n \in N^*$,则$S_{偶}=a_2+a_4+a_6+·s+a_{2n}=\frac{n(a_2+a_{2n})}{2}=na_{n+1}$,$S_{奇}=a_1+a_3+·s+a_{2n-1}=\frac{n(a_1+a_{2n-1})}{2}=na_n$,所以$S_{偶}-S_{奇}=na_{n+1}-na_n=nd$,即$165-220=5d$,解得$d=-11$.若此数列的项数为奇数,设项数为$2n-1$,则$S_{奇}'=a_1+a_3+·s+a_{2n-1}=\frac{n(a_1+a_{2n-1})}{2}=na_n$,$S_{偶}'=a_2+a_4+·s+a_{2n-2}=\frac{(n-1)(a_2+a_{2n-2})}{2}=(n-1)a_n$,所以$\frac{S_{奇}'}{n-1}=\frac{220}{4}=55$.
教材链接 人教A版选择性必修二4.2.2练习1第5题
教材链接 人教A版选择性必修二4.2.2练习1第5题
13. 已知等差数列$ \{ a_{n}\} $的前 $ n $ 项和为 $ S_{n} $,且 $ S_{4}=4S_{2} $,$ a_{2n}=2a_{n}+1(n \in \mathbf{N}^{*}) $.
(1) 求数列$ \{ a_{n}\} $的通项公式;
(2) 若 $ b_{n}=\begin{cases}a_{n}-2,n 为奇数,\\2a_{n}+8,n 为偶数,\end{cases} $设数列$ \{ b_{n}\} $的前 $ n $ 项和为 $ T_{n} $,求 $ T_{2n} $.
(1) 求数列$ \{ a_{n}\} $的通项公式;
(2) 若 $ b_{n}=\begin{cases}a_{n}-2,n 为奇数,\\2a_{n}+8,n 为偶数,\end{cases} $设数列$ \{ b_{n}\} $的前 $ n $ 项和为 $ T_{n} $,求 $ T_{2n} $.
答案:
13. 解:
(1)设等差数列$\{a_n\}$的首项为$a_1$,公差为$d$,由$S_4=4S_2,a_{2n}=2a_n+1$,得$\begin{cases}4a_1+6d=4(2a_1+d),\\a_1+(2n-1)d=2[a_1+(n-1)d]+1,\end{cases}$
化简得$\begin{cases}d=2a_1,\\d=a_1+1,\end{cases}$解得$\begin{cases}a_1=1,\\d=2,\end{cases}$所以数列$\{a_n\}$的通项公式为$a_n=2n-1$.
(2)由$a_n=2n-1$,得$b_n=\begin{cases}2n-3,n为奇数,\\4n+6,n为偶数,\end{cases}$则$T_{2n}=(b_1+b_3+·s+b_{2n-1})+(b_2+b_4+·s+b_{2n})=[-1+3+7+·s+(4n-5)]+[14+22+30+·s+(8n+6)]=(-1+4n-5) · n \frac{1}{2}+(14+8n+6) · n \frac{1}{2}=6n^2+7n$.
(1)设等差数列$\{a_n\}$的首项为$a_1$,公差为$d$,由$S_4=4S_2,a_{2n}=2a_n+1$,得$\begin{cases}4a_1+6d=4(2a_1+d),\\a_1+(2n-1)d=2[a_1+(n-1)d]+1,\end{cases}$
化简得$\begin{cases}d=2a_1,\\d=a_1+1,\end{cases}$解得$\begin{cases}a_1=1,\\d=2,\end{cases}$所以数列$\{a_n\}$的通项公式为$a_n=2n-1$.
(2)由$a_n=2n-1$,得$b_n=\begin{cases}2n-3,n为奇数,\\4n+6,n为偶数,\end{cases}$则$T_{2n}=(b_1+b_3+·s+b_{2n-1})+(b_2+b_4+·s+b_{2n})=[-1+3+7+·s+(4n-5)]+[14+22+30+·s+(8n+6)]=(-1+4n-5) · n \frac{1}{2}+(14+8n+6) · n \frac{1}{2}=6n^2+7n$.
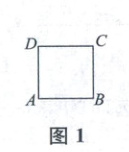
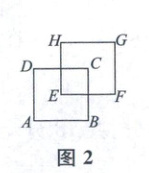
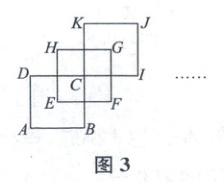
14. (创新·新情境[多选题])边长为 2 个单位长度的正方形 $ ABCD $ 如图 1 所示. 将正方形 $ ABCD $ 向右平移 1 个单位长度,再向上平移 1 个单位长度,得到正方形 $ EFGH $,正方形 $ ABCD $ 和 $ EFGH $ 的组合图形如图 2 所示. 将正方形 $ EFGH $ 向右平移 1 个单位长度,再向上平移 1 个单位长度,得到正方形 $ CIJK $,正方形 $ ABCD $,$ EFGH $ 和 $ CIJK $ 的组合图形如图 3 所示. 依此类推,得到图 $ n(n \in \mathbf{N}^{*}) $,则( )
A.图 3 中矩形的个数为 11
B.图 4 中矩形的个数为 19
C.图 10 中矩形的个数为 81
D.图 1 至图 20 中所有矩形的个数之和为 1 732



A.图 3 中矩形的个数为 11
B.图 4 中矩形的个数为 19
C.图 10 中矩形的个数为 81
D.图 1 至图 20 中所有矩形的个数之和为 1 732
答案:
14. ACD 在图3的正方形$EFGH$中,有$9$个矩形,再加上正方形$ABCD,CIJK$,所以图3中矩形的个数为$11$,故A正确.如图4,在图4的正方形$CIJK$中,有$9$个矩形,与图3中的矩形相比,重合了矩形$CQGR,CIJK$,多了矩形$OISH,PFTK$,再加上正方形$GLMN$,所以图4中矩形的个数为$11+9-2+2+1=21$,故B错误.依此类推,可知从图3开始,往后的每个图形中的矩形都比前一个图形中的矩形多$10$个.设图1、图2、图3、$·s$、图$n$中的矩形个数分别为$a_1,a_2,a_3,·s,a_n$,则从第三项开始,该数列成公差为$10$的等差数列.易得$a_1=1,a_2=3$,所以$a_n=\begin{cases}1, & n=1, \\ 3, & n=2, \\ a_3+(n-3)d=10n-19,n \geqslant 3,\end{cases}$
$81$,故C正确.因为$a_{20}=20 × 10-19=181$,所以图1至图20中所有矩形的个数之和为$a_1+a_2+\frac{(20-2) × (a_3+a_{20})}{2}=1+3+\frac{18 × (11+181)}{2}=1732$,故D正确.
$81$,故C正确.因为$a_{20}=20 × 10-19=181$,所以图1至图20中所有矩形的个数之和为$a_1+a_2+\frac{(20-2) × (a_3+a_{20})}{2}=1+3+\frac{18 × (11+181)}{2}=1732$,故D正确.
查看更多完整答案,请扫码查看


