2025年小题狂做高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
12. (高频导向)《尘劫记》是在元代的《算学启蒙》和明代的《算法统宗》的基础上编撰的一部古典数学著作,其中记载了一个这样的问题:假设每对老鼠每月生子一次,每月生12只,且雌雄各半;1个月后,有一对老鼠生了12只小老鼠,一共有14只;2个月后,每对老鼠各生了12只小老鼠,一共有98只.以此类推,假设$n$个月后共有老鼠$a_{n}$只,则$a_{12} =$ ________.
答案:
12. $2×7^{12}$ 设$n$个月后共有$a_{n}$只老鼠,且雌雄各半,所以$(n + 1)$个月后的老鼠只数$a_{n + 1}$满足$a_{n + 1}=a_{n}+12×\frac{a_{n}}{2}$,即$a_{n + 1}=7a_{n}$.又$a_{1}=14\neq0$,所以$\frac{a_{n + 1}}{a_{n}}=7$,即$\{a_{n}\}$是以$14$为首项,$7$为公比的等比数列,所以$a_{n}=a_{1}q^{n - 1}=14×7^{n - 1}=2×7×7^{n - 1}=2×7^{n}$,即$a_{n}=2×7^{n}$,$a_{12}=2×7^{12}$.
13. 已知数列$\{ a_{n}\}$的首项$a_{1} = \frac{4}{5}$,$a_{n + 1} = \frac{4a_{n}}{3a_{n} + 1}$.
(1) 设$b_{n} = \frac{1}{a_{n}} - 1$,求数列$\{ b_{n}\}$的通项公式.
(2) 是否存在互不相等的正整数$m,s,n$,使得$m,s,n$成等差数列,且$a_{m} - 1,a_{s} - 1,a_{n} - 1$成等比数列?如果存在,请证明;如果不存在,请说明理由.
(1) 设$b_{n} = \frac{1}{a_{n}} - 1$,求数列$\{ b_{n}\}$的通项公式.
(2) 是否存在互不相等的正整数$m,s,n$,使得$m,s,n$成等差数列,且$a_{m} - 1,a_{s} - 1,a_{n} - 1$成等比数列?如果存在,请证明;如果不存在,请说明理由.
答案:
13. 解:
(1)因为$a_{n + 1}=\frac{4a_{n}}{3a_{n}+1}$,$a_{1}=\frac{4}{5}\neq0$,所以$\frac{1}{a_{n + 1}}=\frac{3}{4}+\frac{1}{4a_{n}}$,所以$\frac{1}{a_{n + 1}}-1=\frac{1}{4}(\frac{1}{a_{n}} - 1)$.又$b_{n}=\frac{1}{a_{n}} - 1$,$b_{1}=\frac{1}{a_{1}} - 1=\frac{5}{4}-1=\frac{1}{4}\neq0$,所以$\{b_{n}\}$是以$\frac{1}{4}$为首项,$\frac{1}{4}$为公比的等比数列,所以$b_{n}=\frac{1}{4}×(\frac{1}{4})^{n - 1}=(\frac{1}{4})^{n}(n\in\mathbf{N}^{*})$.
(2)假设存在,则$m + n = 2s$,$(a_{m}-1)·(a_{n}-1)=(a_{s}-1)^{2}$.由
(1)得,$\frac{1}{a_{n}} - 1=(\frac{1}{4})^{n}$,即$a_{n}=\frac{1}{(\frac{1}{4})^{n}+1}=\frac{4^{n}}{4^{n}+1}$,所以$(a_{m}-1)·(a_{n}-1)=(\frac{4^{m}}{4^{m}+1}-1)·(\frac{4^{n}}{4^{n}+1}-1)=(-\frac{1}{4^{m}+1})·(-\frac{1}{4^{n}+1})=\frac{1}{(4^{m}+1)(4^{n}+1)}$,$(a_{s}-1)^{2}=(-\frac{1}{4^{s}+1})^{2}=\frac{1}{(4^{s}+1)^{2}}$,故$\frac{1}{(4^{m}+1)(4^{n}+1)}=\frac{1}{(4^{s}+1)^{2}}$,化简得$4^{m}+4^{n}=2·4^{s}$.因为$4^{m}+4^{n}\geq2·\sqrt{4^{m + n}}=2·4^{s}$,当且仅当$m = n$时等号成立,又$m,s,n$互不相等,所以$4^{m}+4^{n}>2·4^{s}$,即不存在符合条件的$m,s,n$.
解题突破 构造法求数列通项的技巧
对于形如$a_{n + 1}=pa_{n}+q(p\neq1)$型递推公式,通常可构造等比数列$\{a_{n}+x\}(其中x=\frac{q}{p - 1})$来进行求解.
(1)因为$a_{n + 1}=\frac{4a_{n}}{3a_{n}+1}$,$a_{1}=\frac{4}{5}\neq0$,所以$\frac{1}{a_{n + 1}}=\frac{3}{4}+\frac{1}{4a_{n}}$,所以$\frac{1}{a_{n + 1}}-1=\frac{1}{4}(\frac{1}{a_{n}} - 1)$.又$b_{n}=\frac{1}{a_{n}} - 1$,$b_{1}=\frac{1}{a_{1}} - 1=\frac{5}{4}-1=\frac{1}{4}\neq0$,所以$\{b_{n}\}$是以$\frac{1}{4}$为首项,$\frac{1}{4}$为公比的等比数列,所以$b_{n}=\frac{1}{4}×(\frac{1}{4})^{n - 1}=(\frac{1}{4})^{n}(n\in\mathbf{N}^{*})$.
(2)假设存在,则$m + n = 2s$,$(a_{m}-1)·(a_{n}-1)=(a_{s}-1)^{2}$.由
(1)得,$\frac{1}{a_{n}} - 1=(\frac{1}{4})^{n}$,即$a_{n}=\frac{1}{(\frac{1}{4})^{n}+1}=\frac{4^{n}}{4^{n}+1}$,所以$(a_{m}-1)·(a_{n}-1)=(\frac{4^{m}}{4^{m}+1}-1)·(\frac{4^{n}}{4^{n}+1}-1)=(-\frac{1}{4^{m}+1})·(-\frac{1}{4^{n}+1})=\frac{1}{(4^{m}+1)(4^{n}+1)}$,$(a_{s}-1)^{2}=(-\frac{1}{4^{s}+1})^{2}=\frac{1}{(4^{s}+1)^{2}}$,故$\frac{1}{(4^{m}+1)(4^{n}+1)}=\frac{1}{(4^{s}+1)^{2}}$,化简得$4^{m}+4^{n}=2·4^{s}$.因为$4^{m}+4^{n}\geq2·\sqrt{4^{m + n}}=2·4^{s}$,当且仅当$m = n$时等号成立,又$m,s,n$互不相等,所以$4^{m}+4^{n}>2·4^{s}$,即不存在符合条件的$m,s,n$.
解题突破 构造法求数列通项的技巧
对于形如$a_{n + 1}=pa_{n}+q(p\neq1)$型递推公式,通常可构造等比数列$\{a_{n}+x\}(其中x=\frac{q}{p - 1})$来进行求解.
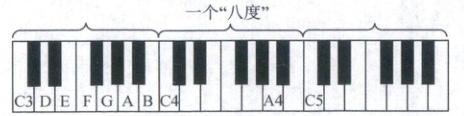
14. (创新·新情境[多选题]我国明代音乐理论家和数学家朱载堉在所著的《律学新说》一书中提出了“十二平均率”的音乐理论,该理论后被意大利传教士利玛窦带到西方,对西方的音乐产生了深远的影响.以钢琴为首的众多键盘乐器就是基于“十二平均率”的理论指导设计的.图中钢琴上的每12个琴键(7个白键5个黑键)构成一个“八度”,每个“八度”各音阶的音高都是前一个“八度”对应音阶的两倍,如图中所示的琴键的音高C5 = 2·C4(C4称为“中央C”).将每个“八度”(如C4与C5之间的音高变化)按等比数列十二等分,得到钢琴上88个琴键的音阶.当钢琴的A4键调为标准音440 Hz时,此时钢琴发出的音的频率(单位:Hz)可以是
( )(参考数据:$2^{\frac{1}{12}} = 1.414$,$2^{\frac{1}{4}} = 1.260$,$2^{\frac{1}{3}} = 1.189$,$2^{\frac{5}{12}} = 1.148$,$2^{\frac{1}{2}} = 1.122$,$2^{\frac{12}{12}} = 1.059$)
A.110
B.233
C.505
D.1244
( )(参考数据:$2^{\frac{1}{12}} = 1.414$,$2^{\frac{1}{4}} = 1.260$,$2^{\frac{1}{3}} = 1.189$,$2^{\frac{5}{12}} = 1.148$,$2^{\frac{1}{2}} = 1.122$,$2^{\frac{12}{12}} = 1.059$)

A.110
B.233
C.505
D.1244
答案:
14. ABD 因为A4 = 440,$\frac{440}{110}=4 = 2^{2}$,所以110 Hz是A4往左两个“八度”A2键的音,故A正确;设相邻音阶的公比为$q$,则$\frac{C5}{C4}=2 = q^{12}$,所以$q = 2^{\frac{1}{12}}$,而A3 = 220,A4 = 440,A5 = 880,$\frac{233}{220}\approx1.059 = 2^{\frac{1}{12}}=q$,故B正确;$\frac{505}{440}\approx1.148=2^{\frac{5}{12}}=q^{5}$,故C错误;$\frac{1244}{880}\approx1.414 = 2^{\frac{1}{2}}=q^{6}$,故D正确.
查看更多完整答案,请扫码查看


