《2025年小题狂做高中数学选择性必修第二册人教版》

9. $[2025$ 湖北部分省级示范高中期中$]$烟花三月,莺飞草长,美丽的樱花开满园.将樱花抽象成几何图形,并按照一定的规律循环,如图:

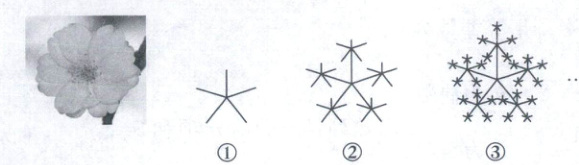
图①将樱花抽象后,得樱花数$a _ { 1 } = 1$,图②以樱花五片花瓣为蕊作五个缩小版樱花,得樱花数$a _ { 2 } = 6$,以此类推.假设第$n$个图的樱花数是$a _ { n }$,设数列$\{ a _ { n } \}$的前$n$项和为$S _ { n }$,则下列说法正确的是
( )

A.$a _ { n } = 6 a _ { n - 1 } ( n \geq 2 , n \in \mathbf { N } ^ { * } )$
B.$S _ { n } = \frac { 5 ^ { n + 1 } - 5 } { 1 6 } - \frac { n } { 4 }$
C.数列$\{ \frac { S _ { n } } { n } \}$是递增数列
D.数列$\{ \frac { 5 ^ { n } } { a _ { n } a _ { n + 1 } } \}$的前$n$项和为$1 - \frac { 4 } { 5 ^ { n + 1 } - 1 }$

答案： BCD

10. $[2025$ 河北石家庄联考$]$已知数列$\{ a _ { n } \}$中,$a _ { n } = 4 × ( - 1 ) ^ { n - 1 } - n ( n \in \mathbf { N } ^ { * } )$,则数列$\{ a _ { n } \}$的前$2 n$项和$S _ { 2 n } =$______.

答案： $10. -2n^{2}-n $数列$\{a_{n}\}$的前 2n 项和$ S_{2n}=a_{1}+a_{2}+a_{3}+·s+a_{2n}=4×[(-1)^{0}+(-1)^{1}+(-1)^{2}+·s+(-1)^{2n - 1}]-(1 + 2 + 3+·s+2n)=4×0-\frac{2n(1 + 2n)}{2}=-2n^{2}-n。$

11. $[2025$ 福建福州期末$]$某汽车集团计划大力发展新能源汽车,2024年全年生产新能源汽车10 000辆.如果在后续的几年中,后一年的产量在前一年的基础上提高20%,那么2032年全年生产新能源汽车约______辆.(参考数据:$1 . 2 ^ { 7 } \approx 3 . 5 8 , 1 . 2 ^ { 8 } \approx 4 . 3 0 , 1 . 2 ^ { 9 } \approx 5 . 1 6$)

答案： 11. 43 000 根据题意，从 2024 年开始，每一年新能源汽车产量构成等比数列$\{a_{n}\}，$且$ a_{1}=10 000，$公比 q = 1 + 20\% = 1.2，所以$ a_{n}=a_{1}q^{n - 1}=10 000×1.2^{n - 1}，$则$ a_{9}=10 000×1.2^{8}\approx43 000，$故 2032 年全年生产新能源汽车约 43 000 辆。

12. $[2025$ 湖北荆、荆、襄、宜四地七校期中联考$]$已知递增数列$\{ a _ { n } \}$的各项均是正整数,且满足$a _ { a _ { n } } = 3 n$,则$a _ { 1 } =$______,$a _ { 9 } + a _ { 1 0 } =$______.

答案： 12. 2 37 由已知$ a_{4}=3，$若$ a_{1}=1，$则$ a_{1}=3，$矛盾；若$ a_{1}=k \geq 3，$则$ a_{k}=a_{a_{1}}=3 \leq a_{1}，$与$\{a_{n}\}$是递增数列矛盾，故$ a_{1}=2。$由$ a_{1}=2，$得$ a_{2}=a_{a_{1}}=3，$$a_{3}=a_{a_{2}}=6，$所以$ a_{6}=a_{a_{3}}=9，$$a_{9}=a_{a_{6}}=18；$又$ a_{3} ＜ a_{4} ＜ a_{5} ＜ a_{6}，$则$ 6 ＜ a_{4} ＜ a_{5} ＜ 9，$所以$ a_{4}=7，$$a_{5}=8，$故$ a_{7}=a_{a_{4}}=12，$$a_{12}=a_{a_{7}}=21，$则由$ a_{9} ＜ a_{10} ＜ a_{11} ＜ a_{12}，$即$ 18 ＜ a_{10} ＜ a_{11} ＜ 21，$知$ a_{10}=19，$故$ a_{9}+a_{10}=37。$

13. $[2025$ 广东佛山联考$]$已知$S _ { n }$是等差数列$\{ a _ { n } \}$的前$n$项和,且$S _ { n } + S _ { n + 1 } = n ^ { 2 } + 2 n + 1$.
(1) 求$\{ a _ { n } \}$的通项公式;
(2) 若$b _ { n } = 3 ^ { a _ { n } - 1 }$,求数列$\{ a _ { n } b _ { n } \}$的前$n$项和$T _ { n }$.

答案： 13. 解：
(1)设等差数列$\{a_{n}\}$的公差为 d。由$ S_{n}+S_{n + 1}=n^{2}+2n + 1=(n + 1)^{2}，$可得$ S_{n + 1}+S_{n + 2}=(n + 2)^{2}，$两式相减可得$ a_{n + 1}+a_{n + 2}+a_{n + 3}=2(n + 1)+3，$两式相减可得$ 2d=(a_{n + 2}+a_{n + 3})-(a_{n + 1}+a_{n + 2})=2，$即 d = 1。当 n = 1 时，$S_{1}+S_{2}=2a_{1}+a_{2}=3a_{1}+d = 4，$解得$ a_{1}=1，$所以$ a_{n}=1+(n - 1)×1=n，$故$\{a_{n}\}$的通项公式为$ a_{n}=n。$
(2)由
(1)知$ b_{n}=3^{a_{n}-1}=3^{n - 1}，$则$ a_{n}b_{n}=n·3^{n - 1}，$故$ T_{n}=1×3^{0}+2×3^{1}+·s+n·3^{n - 1} ①，$①×3 得$ 3T_{n}=1×3^{1}+3^{2}+·s+3^{n - 1}-n·3^{n}=\frac{1 - 3^{n}}{1 - 3}-n·3^{n}=\frac{3^{n}-1}{2}-n·3^{n}，$故$ T_{n}=\frac{(2n - 1)·3^{n}+1}{4}$