《2025年综合应用创新题典中点五年级数学上册西师大版》

(1) 一个平行四边形的底是 $3.6\mathrm{m}$,高是 $2.8\mathrm{m}$,这个平行四边形的面积是（10.08）$\mathrm{m}^2$,和它等底等高的三角形的面积是（5.04）$\mathrm{m}^2$。

答案： 10.08 5.04

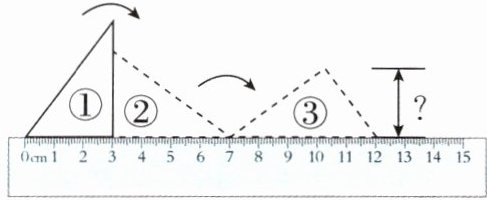
(2) 新考法 数形结合法 如下图,聪聪把一块直角三角形硬纸板放在直尺上绕顶点向右翻滚(从①→②→③),此时它的高度是（2.4）$\mathrm{cm}$。

答案： 2.4

(3) 如图,梯形的面积是 $120\mathrm{cm}^2$,则涂色部分的面积是（40）$\mathrm{cm}^2$。

答案： 40

(4) 一个梯形的上底是 $20\mathrm{cm}$,把下底缩短 $6\mathrm{cm}$ 就变成了一个平行四边形,这时面积减少了 $24\mathrm{cm}^2$,原来梯形的面积是（184）$\mathrm{cm}^2$。

答案： 184 [点拨]梯形下底缩短后变成平行四边形，可知梯形的下底就是(20+6)cm,且减少的是一个三角形的面积。逆用三角形面积公式，求出三角形的高=三角形的面积×2÷底，也就是梯形的高，再代入梯形面积公式求解即可。

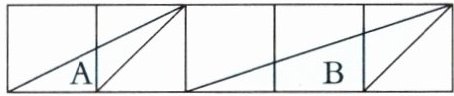
(5) 如下图,在边长相等的五个正方形中,画了两个三角形。若三角形 $A$ 的面积是 $45\mathrm{cm}^2$,则三角形 $B$ 的面积是（90）$\mathrm{cm}^2$。

答案： 90

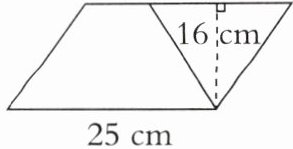
(6) 用两个完全相同的直角梯形正好拼成一个正方形,已知直角梯形的上底是 $15\mathrm{cm}$,下底是 $25\mathrm{cm}$,则梯形的面积是（800）$\mathrm{cm}^2$。

答案： 800 [点拨]两个完全相同的直角梯形正好拼成一个正方形，则正方形的边长就是梯形的上、下底之和，也是梯形的高，所以梯形的面积是(15+25)×(15+25)÷2=800(cm²)。

(7) 一条线段把平行四边形分成梯形与三角形两个部分,其中梯形面积比三角形面积大 $168\mathrm{cm}^2$,梯形的上底是（）$\mathrm{cm}$。

答案：
10.5 [点拨]如图，将线段向左平移，可知梯形比三角形的面积多出一个平行四边形，这个平行四边形的底为梯形的上底，高为平行四边形的高，因此梯形的上底为168÷16=10.5(cm)。

(1) 一个三角形,底扩大到原来的 4 倍,高缩小到原来的一半,这个三角形的面积(D)。
A.扩大到原来的 4 倍
B.缩小到原来的一半
C.不变
D.扩大到原来的 2 倍

答案： D

(2) 成都市成华区期末 公园里有一块平行四边形空地,绿化部门打算一半种鲜花(涂色部分),一半铺草坪(空白部分)。设计小组提供了几种方案,符合绿化部门要求的有(D)种。

A.$2$
B.$3$
C.$4$
D.$5$

答案： D

(3) 如下图,三个涂色图形的面积相比,(B)。

A.三角形的面积最大
B.平行四边形的面积最大
C.梯形的面积最大
D.无法比较

答案： B [点拨]由图可知，三个图形等高，设它们的高为h,则三角形的面积是15×h÷2=7.5h,平行四边形的面积是8h,梯形的面积是(2+13)×h÷2=7.5h,8h＞7.5h,所以平行四边形的面积最大。

(4) 下列说法错误的是(B)。
A.同底等高的三角形,它们的形状不一定相同,但面积一定相等
B.平行四边形的面积是三角形面积的 $2$ 倍
C.把一个平行四边形任意分割成两个梯形,这两个梯形的高一定相等
D.一个梯形的上、下底的和不变,高扩大到原来的 $2$ 倍,则面积也扩大到原来的 $2$ 倍

答案： B

(5) 如图,把三角形 $ABC$ 的边 $AB$ 延长 $1$ 倍到点 $D$,把另一边 $AC$ 延长 $2$ 倍到点 $E$,得到三角形 $ADE$,三角形 $ADE$ 的面积是三角形 $ABC$ 的(6)倍。

A.$2$
B.$4$
C.$5$
D.$6$

答案： D [点拨]连接BE,因为AB=BD,AE=3AC,所以三角形ABE的面积=三角形ABC的面积×3,三角形ADE的面积=三角形ABE的面积×2,所以三角形ADE的面积=三角形ABC的面积×3×2=三角形ABC的面积×6,即三角形ADE的面积是三角形ABC 的6倍。