《2025年课本配套练习六年级数学上册苏教版》

1. 棱长5分米的正方体的表面积是( )平方分米，体积是( )立方分米，棱长总和是( )分米。

答案： 150，125，60

2. 用一根48分米长的铁丝焊接成一个正方体框架，这个正方体的底面积是()平方分米，体积是()立方分米。

答案： 底面积答案填16，体积答案填64，由于设置的是填空形式，按照两个空顺序，答案分别为（16），（64）。

3. 一个长方体的棱长总和是2.4米，这个长方体相交于同一顶点的三条棱的长度之和是()米。

答案： 0.6

4. 用3个棱长2分米的正方体摆成一个长方体，这个长方体的体积是()立方分米，表面积是()平方分米。

答案： 24，56

5. 一个长方体的长、宽、高分别是10分米、6分米、5分米，这个长方体相邻两个面的面积最多相差()平方分米，表面积是()平方分米，所占空间是()立方分米。

答案： 30；280；300

6. 把一个长24厘米、宽18厘米、高9厘米的长方体木块截成棱长3厘米的正方体木块(不许有剩余)，可以截成()个。

答案： 144

7. 把20升水倒入一个棱长5分米的正方体容器中，水深()分米。

答案： 0.8（或写成$\frac{4}{5}$，根据题目空白处填写形式确定，如果为小数填0.8 ，若为分数填$\frac{4}{5}$ ）

8. 用丝带捆扎一个长、宽、高分别是30厘米、20厘米、10厘米的长方体礼品盒(如图)，打结处用去丝带25厘米，需要准备()分米长的丝带。

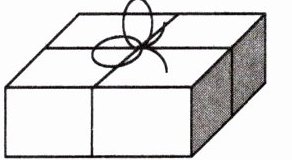
答案： 16.5

9. 摆一个棱长1分米的正方体，需要1立方厘米的小正方体()块，摆成的正方体的表面积是()平方厘米。

答案： 1000；600

10. 一个长方体，长减少到原来的一半，宽增加到原来的3倍，高增加到原来的2倍，体积增加到原来的()倍。

答案： 3

11. 一个正方体蓄水池，从里面量，长、宽、高都是1米，装满水时，水的()是1立方米。

答案： 体积

12. 把一个棱长6厘米的正方体切割成3个完全一样的长方体，每个长方体的体积是()立方厘米，表面积是()平方厘米。

答案： 72，120

13. 用几个棱长1分米的正方体摆成如图所示的物体，这个物体的体积是()立方分米，表面积是()平方分米。

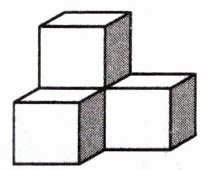
答案： 4，18

1. 造一个长50米、宽30米、深2米的长方体游泳池。
(1)这个游泳池占地多少平方米？
(2) 绕着游泳池走一圈,至少要走多少米?
(3) 如果在游泳池的四壁和底面贴上边长 2 分米的正方形瓷砖,需要贴多少块?

答案： $(1)$求游泳池占地面积
解：游泳池占地面积就是求这个长方体的底面积，长方体底面积公式为$S = a× b$（$a$为长，$b$为宽）。
已知$a = 50$米，$b = 30$米，代入公式可得：$S=50×30 = 1500$（平方米）
$(2)$求绕游泳池走一圈的长度
解：绕着游泳池走一圈的长度就是求这个长方体上面的周长，长方形周长公式为$C=(a + b)×2$（$a$为长，$b$为宽）。
已知$a = 50$米，$b = 30$米，代入公式可得：$C=(50 + 30)×2=80×2 = 160$（米）
$(3)$求贴瓷砖的块数
解：
步骤一：求需要贴瓷砖的面积
需要贴瓷砖的是游泳池的四壁和底面，其面积为$S = ab+(ah + bh)×2$（$a$为长，$b$为宽，$h$为高）。
已知$a = 50$米，$b = 30$米，$h = 2$米，代入可得：
$S=50×30+(50×2 + 30×2)×2$
$=1500+(100 + 60)×2$
$=1500 + 160×2$
$=1500 + 320$
$=1820$（平方米）
步骤二：求每块瓷砖的面积
已知瓷砖为边长$2$分米的正方形，根据正方形面积公式$S_{砖}=c× c$（$c$为边长），先将单位换算为米，$2$分米$ = 0.2$米，则$S_{砖}=0.2×0.2 = 0.04$（平方米）
步骤三：求瓷砖块数
瓷砖块数$n=\frac{S}{S_{砖}}$，将$S = 1820$平方米，$S_{砖}=0.04$平方米代入可得：$n=\frac{1820}{0.04}=45500$（块）
综上，答案依次为：$(1)$$\boldsymbol{1500}$平方米；$(2)$$\boldsymbol{160}$米；$(3)$$\boldsymbol{45500}$块。