《2025年课本配套练习六年级数学上册苏教版》

1. 长方体和正方体都有()个面、()条棱、()个顶点。

答案： 6,12,8

2. 正方体是特殊的( )，它所有棱的长度( )，所有面的面积( )。

答案： 长方体；相等；相等

3. 至少()个完全一样的小正方体才能拼成一个大正方体。

答案： $8$

4. 一个正方体的底面周长是24厘米，这个正方体的表面积是()平方厘米。

答案： 216

5. 一个长方体的长是10厘米，宽是8厘米，高是6厘米，它右面的面积是()平方厘米，前面的面积是()平方厘米，这个长方体()面或()面的面积是80平方厘米。

答案： 48,60,上,下

6. 一个正方体的棱长总和是36厘米，这个正方体的体积是()立方厘米。

答案： 27

7. 用一根52厘米长的铁丝，正好能焊接成一个长6厘米、宽4厘米、高()厘米的长方体框架。

答案： 3

8. 将60升水倒入一个长6分米、宽2.5分米的长方体水箱，正好倒满，这个水箱深()分米。

答案： $4$

9. 一个棱长1米的大正方体能切割成()个棱长1分米的小正方体。如果把这些小正方体顺次紧紧地排成一行，能排()米。

答案： 1000，100

10. 根据长方体摆放的位置，在对应的展开图中标出各个面的名称。

答案：

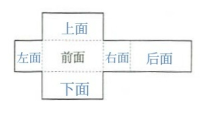
二、判断是非。
1. 两个正方体的棱长总和相等，它们的表面积一定相等。 ()
2. 棱长6厘米的正方体的表面积和体积相等。 ()
3. 金鱼缸的容积大约是20平方分米。 ()
4. 一个正方体的棱长增加到原来的3倍，那么它的表面积增加到原来的6倍，体积增加到原来的9倍。 ()
5. 一个厚玻璃瓶的体积是3立方分米，瓶里一定能装3升水。 ()

答案： 1. √
2. ×
3. ×
4. ×
5. ×

1. 一个正方体的棱长是3分米，它的表面积和体积各是多少？

答案： 答题卡：
表面积：
公式：表面积 = 6 × (棱长)$^2$
代入：$6 × 3^2 = 6 × 9 = 54$（平方分米）
体积：
公式：体积 = (棱长)$^3$
代入：$3^3 = 27$（立方分米）
结论：
表面积：54平方分米；
体积：27立方分米。