第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
实验 测量物体运动的平均速度
| | |
| 实验操作 | 间接测量法,用刻度尺测量物体运动的距离$s$,用秒表测出物体运动的时间$t$,测量原理是$v= \frac{s}{t}$(1)测出小车在全程的平均速度$v_{1}= \frac{s_{1}}{t_{1}}$(2)测出小车在前半程的平均速度$v_{2}= \frac{s_{2}}{t_{2}}$(3)测出小车在后半程的平均速度$v_{3}= \frac{s_{1}-s_{2}}{t_{1}-t_{2}}$(4)比较$v_{1}$、$v_{2}$、$v_{3}$的大小 |
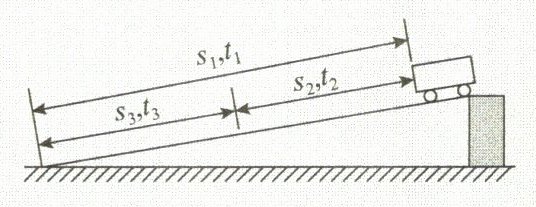
| 注意事项 | (1)斜面倾角要小一些,便于测量时间(2)测量过程中不要改变斜面的倾角,以便将分段测量和整体分析统一起来 |
| 评估交流 | (1)与其他同学的结果比较,所测得的平均速度大小不相同,其原因可能是斜面倾角不同、选取路段不同等(2)若放开小车后一会儿再开始计时,则测得的速度偏大 |
| 深入拓展 | (1)$v_{3}>v_{2}$,说明小车下滑的速度越来越大,即小车做加速直线运动(2)$v_{1}$、$v_{2}$、$v_{3}$不相等,说明小车在不同路段的平均速度不相等,故计算平均速度时$s与t$必须一一对应 |
例 小明同学做“测量物体运动的平均速度”的实验,图1-8是实验时小车从斜面顶端滑下的示意图。
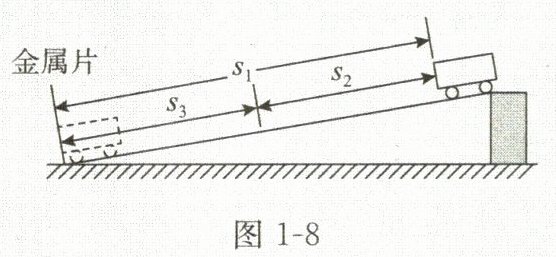
(1)在该实验中,应该用______测量小车通过的路程$s$,用______测量小车运动的时间$t$,通过公式______求出平均速度$v$。
(2)实验中,斜面应保持______(填“较小”“较大”或“很大”)的坡度,这是为了便于测量______。
(3)下表是他未完成的记录,请你将表填写完整。
| 路程$s/cm$ | 运行时间$t/s$ | 平均速度$v/(cm\cdot s^{-1})$ |
| $s_{1}= 80.0$ | $t_{1}= 2.8$ | $v_{1}= 28.6$ |
| $s_{2}= 40.0$ | $t_{2}= 2.0$ | $v_{2}= 20.0$ |
| $s_{3}= 40.0$ | $t_{3}= $______ | $v_{3}= $______ |

| | |
| 实验操作 | 间接测量法,用刻度尺测量物体运动的距离$s$,用秒表测出物体运动的时间$t$,测量原理是$v= \frac{s}{t}$(1)测出小车在全程的平均速度$v_{1}= \frac{s_{1}}{t_{1}}$(2)测出小车在前半程的平均速度$v_{2}= \frac{s_{2}}{t_{2}}$(3)测出小车在后半程的平均速度$v_{3}= \frac{s_{1}-s_{2}}{t_{1}-t_{2}}$(4)比较$v_{1}$、$v_{2}$、$v_{3}$的大小 |

| 注意事项 | (1)斜面倾角要小一些,便于测量时间(2)测量过程中不要改变斜面的倾角,以便将分段测量和整体分析统一起来 |
| 评估交流 | (1)与其他同学的结果比较,所测得的平均速度大小不相同,其原因可能是斜面倾角不同、选取路段不同等(2)若放开小车后一会儿再开始计时,则测得的速度偏大 |
| 深入拓展 | (1)$v_{3}>v_{2}$,说明小车下滑的速度越来越大,即小车做加速直线运动(2)$v_{1}$、$v_{2}$、$v_{3}$不相等,说明小车在不同路段的平均速度不相等,故计算平均速度时$s与t$必须一一对应 |
例 小明同学做“测量物体运动的平均速度”的实验,图1-8是实验时小车从斜面顶端滑下的示意图。

(1)在该实验中,应该用______测量小车通过的路程$s$,用______测量小车运动的时间$t$,通过公式______求出平均速度$v$。
(2)实验中,斜面应保持______(填“较小”“较大”或“很大”)的坡度,这是为了便于测量______。
(3)下表是他未完成的记录,请你将表填写完整。
| 路程$s/cm$ | 运行时间$t/s$ | 平均速度$v/(cm\cdot s^{-1})$ |
| $s_{1}= 80.0$ | $t_{1}= 2.8$ | $v_{1}= 28.6$ |
| $s_{2}= 40.0$ | $t_{2}= 2.0$ | $v_{2}= 20.0$ |
| $s_{3}= 40.0$ | $t_{3}= $______ | $v_{3}= $______ |

答案:
(1)刻度尺 秒表 v = $\frac{s}{t}$
(2)较小 时间
(3)0.8 50.0【解析】
(1)在该实验中,用刻度尺测量小车通过的路程,用秒表测量小车运动的时间,根据速度的公式v = $\frac{s}{t}$得到平均速度,测量小车平均速度的原理是v = $\frac{s}{t}$。
(2)斜面的倾角越小(坡度越小),小车运动时间越长,便于测量小车的运动时间,所以实验中斜面应保持较小坡度。
(3)根据表格数据可知t₃ = t₁ - t₂ = 2.8 s - 2.0 s = 0.8 s,平均速度v₃ = $\frac{s₃}{t₃}$ = $\frac{40.0\ cm}{0.8\ s}$ = 50.0 cm/s。
(1)刻度尺 秒表 v = $\frac{s}{t}$
(2)较小 时间
(3)0.8 50.0【解析】
(1)在该实验中,用刻度尺测量小车通过的路程,用秒表测量小车运动的时间,根据速度的公式v = $\frac{s}{t}$得到平均速度,测量小车平均速度的原理是v = $\frac{s}{t}$。
(2)斜面的倾角越小(坡度越小),小车运动时间越长,便于测量小车的运动时间,所以实验中斜面应保持较小坡度。
(3)根据表格数据可知t₃ = t₁ - t₂ = 2.8 s - 2.0 s = 0.8 s,平均速度v₃ = $\frac{s₃}{t₃}$ = $\frac{40.0\ cm}{0.8\ s}$ = 50.0 cm/s。
1. 小明用小车、长木板、刻度尺、秒表、木块等器材探究小车沿斜面下滑时速度的变化。实验设计如图1-9所示,让小车从斜面的$A$点由静止下滑并开始计时,分别测出小车到达$B点和C点的时间t_{B}$、$t_{C}$。
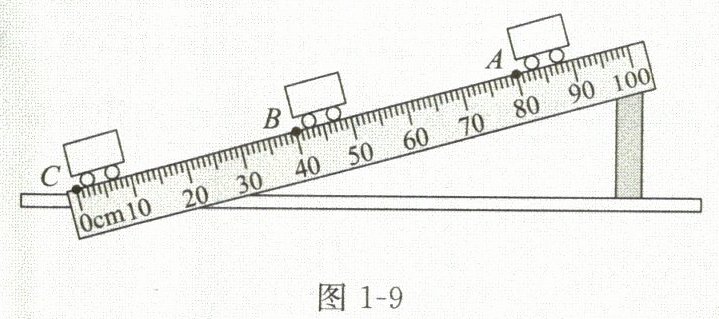
(1)由图可知,斜面上的刻度尺的分度值为______$cm$。
(2)该实验的原理是______。
(3)实验时,为了使小车在斜面上运动的时间更长,应______(填“增大”或“减小”)斜面的坡度。
(4)经测量,$AB$、$BC$段的长度均为______$cm$,$t_{B}= 3.0s$,$t_{C}= 5.0s$,则小车在$AC$段的平均速度为______$cm/s$。
(5)由以上可知:小车在从斜面上$A$点下滑的过程中是做______(填“匀速”或“变速”)直线运动;图1-10所示的$v-t$图像中能反映出小车运动情况的是______(填字母代号)。

(6)实验前必须学会熟练使用电子表,如果在小车过了$A$点后才开始计时,则会使测得的$AC段的平均速度v_{AC}$______(填“偏大”或“偏小”)。
(7)小明进一步实验测得小车在斜面上运动时前半段时间的平均速度为$v_{1}$,后半段时间的平均速度为$v_{2}$,则小车全程的平均速度为______(用字母$v_{1}和v_{2}$表示)。

(1)由图可知,斜面上的刻度尺的分度值为______$cm$。
(2)该实验的原理是______。
(3)实验时,为了使小车在斜面上运动的时间更长,应______(填“增大”或“减小”)斜面的坡度。
(4)经测量,$AB$、$BC$段的长度均为______$cm$,$t_{B}= 3.0s$,$t_{C}= 5.0s$,则小车在$AC$段的平均速度为______$cm/s$。
(5)由以上可知:小车在从斜面上$A$点下滑的过程中是做______(填“匀速”或“变速”)直线运动;图1-10所示的$v-t$图像中能反映出小车运动情况的是______(填字母代号)。

(6)实验前必须学会熟练使用电子表,如果在小车过了$A$点后才开始计时,则会使测得的$AC段的平均速度v_{AC}$______(填“偏大”或“偏小”)。
(7)小明进一步实验测得小车在斜面上运动时前半段时间的平均速度为$v_{1}$,后半段时间的平均速度为$v_{2}$,则小车全程的平均速度为______(用字母$v_{1}和v_{2}$表示)。
答案:
(1)1
(2)v = $\frac{s}{t}$
(3)减小
(4)40.0 16.0
(5)变速 C
(6)偏大
(7)$\frac{v₁ + v₂}{2}$
(1)1
(2)v = $\frac{s}{t}$
(3)减小
(4)40.0 16.0
(5)变速 C
(6)偏大
(7)$\frac{v₁ + v₂}{2}$
查看更多完整答案,请扫码查看


