第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
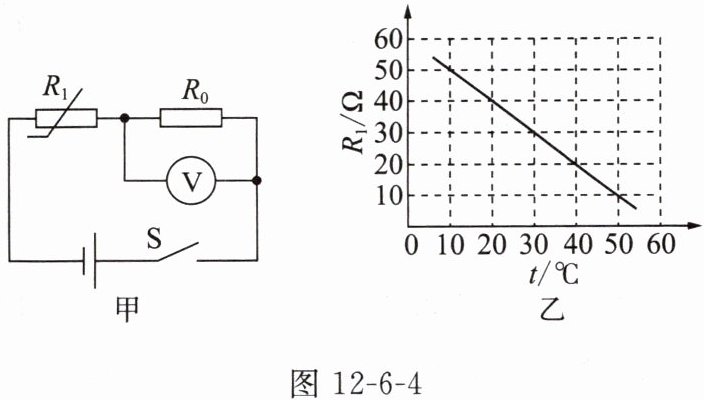
3. 某同学利用热敏电阻设计了如图 12-6-4 甲所示的电路,用来实时监测某一环境的温度,已知电源电压不变,定值电阻 $ R_{0}= 20\ \Omega $,$ R_{1} $是热敏电阻,其阻值随温度变化的关系图像如图 12-6-4 乙所示。
(1)当环境温度为 $ 20^{\circ}C $时,电压表的示数为 $ 2\ V $,电源电压是多大?
(2)当温度在 $ 10\sim50^{\circ}C $范围内变化时,请推导电压表示数 $ U $与环境温度 $ t $的关系式。
(1)当环境温度为 $ 20^{\circ}C $时,电压表的示数为 $ 2\ V $,电源电压是多大?
(2)当温度在 $ 10\sim50^{\circ}C $范围内变化时,请推导电压表示数 $ U $与环境温度 $ t $的关系式。

答案:
$(1)$ 求电源电压
- 解:由电路图可知,$R_{1}$与$R_{0}$串联,电压表测$R_{0}$两端的电压。
当环境温度为$20^{\circ}C$时,由图乙可知,此时热敏电阻的阻值$R_{1}=40\ \Omega$。
根据欧姆定律$I = \frac{U}{R}$,可得此时电路中的电流$I=\frac{U_{0}}{R_{0}}=\frac{2\ V}{20\ \Omega}=0.1\ A$。
因为串联电路中总电阻等于各分电阻之和,所以根据$U = IR$可得电源电压$U = I(R_{1}+R_{0})=0.1\ A×(40\ \Omega + 20\ \Omega)=6\ V$。
$(2)$ 推导电压表示数$U$与环境温度$t$的关系式
- 解:设$R_{1}$与$t$的关系式为$R_{1}=kt + b$。
由图乙可知,当$t_{1}=10^{\circ}C$时,$R_{11}=50\ \Omega$;当$t_{2}=50^{\circ}C$时,$R_{12}=10\ \Omega$。
将$\begin{cases}t_{1}=10^{\circ}C,R_{11}=50\ \Omega\\t_{2}=50^{\circ}C,R_{12}=10\ \Omega\end{cases}$代入$R_{1}=kt + b$得:
$\begin{cases}50 = 10k + b\\10 = 50k + b\end{cases}$
用第一个式子减去第二个式子消去$b$可得:
$50 - 10=(10k + b)-(50k + b)$
$40=-40k$,解得$k = - 1$。
把$k = - 1$代入$50 = 10k + b$得:$50 = 10×(-1)+b$,解得$b = 60$。
所以$R_{1}=-t + 60$。
电路中的电流$I=\frac{U}{R_{1}+R_{0}}=\frac{6}{-t + 60 + 20}=\frac{6}{80 - t}$。
电压表示数$U = IR_{0}=\frac{6}{80 - t}×20=\frac{120}{80 - t}(10^{\circ}C\leq t\leq50^{\circ}C)$。
综上,答案依次为:$(1)$$\boldsymbol{6\ V}$;$(2)$$\boldsymbol{U=\frac{120}{80 - t}(10^{\circ}C\leq t\leq50^{\circ}C)}$。
- 解:由电路图可知,$R_{1}$与$R_{0}$串联,电压表测$R_{0}$两端的电压。
当环境温度为$20^{\circ}C$时,由图乙可知,此时热敏电阻的阻值$R_{1}=40\ \Omega$。
根据欧姆定律$I = \frac{U}{R}$,可得此时电路中的电流$I=\frac{U_{0}}{R_{0}}=\frac{2\ V}{20\ \Omega}=0.1\ A$。
因为串联电路中总电阻等于各分电阻之和,所以根据$U = IR$可得电源电压$U = I(R_{1}+R_{0})=0.1\ A×(40\ \Omega + 20\ \Omega)=6\ V$。
$(2)$ 推导电压表示数$U$与环境温度$t$的关系式
- 解:设$R_{1}$与$t$的关系式为$R_{1}=kt + b$。
由图乙可知,当$t_{1}=10^{\circ}C$时,$R_{11}=50\ \Omega$;当$t_{2}=50^{\circ}C$时,$R_{12}=10\ \Omega$。
将$\begin{cases}t_{1}=10^{\circ}C,R_{11}=50\ \Omega\\t_{2}=50^{\circ}C,R_{12}=10\ \Omega\end{cases}$代入$R_{1}=kt + b$得:
$\begin{cases}50 = 10k + b\\10 = 50k + b\end{cases}$
用第一个式子减去第二个式子消去$b$可得:
$50 - 10=(10k + b)-(50k + b)$
$40=-40k$,解得$k = - 1$。
把$k = - 1$代入$50 = 10k + b$得:$50 = 10×(-1)+b$,解得$b = 60$。
所以$R_{1}=-t + 60$。
电路中的电流$I=\frac{U}{R_{1}+R_{0}}=\frac{6}{-t + 60 + 20}=\frac{6}{80 - t}$。
电压表示数$U = IR_{0}=\frac{6}{80 - t}×20=\frac{120}{80 - t}(10^{\circ}C\leq t\leq50^{\circ}C)$。
综上,答案依次为:$(1)$$\boldsymbol{6\ V}$;$(2)$$\boldsymbol{U=\frac{120}{80 - t}(10^{\circ}C\leq t\leq50^{\circ}C)}$。
1. 交管部门定期开展交通违法专项治理行动。图 12-6-5 甲是查处酒驾行为时使用的某酒精测试仪的工作原理图,电源电压恒定,$ R_{1} $为定值电阻,$ R_{2} $为气敏电阻,其阻值随气体酒精浓度变化的情况如图 12-6-5 乙所示。闭合开关 $ S $,下列说法正确的是(
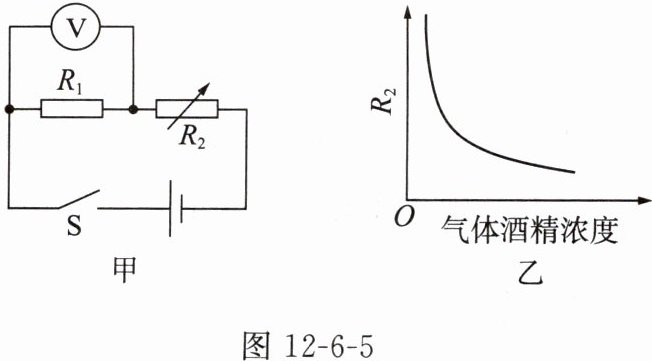
A.气敏电阻 $ R_{2} $是由超导体材料制成的
B.检测的气体酒精浓度越小,电压表的示数越小
C.检测的气体酒精浓度越大,$ R_{2} $的阻值越大
D.检测的气体酒精浓度越大,电路中的电流越小
B
)。
A.气敏电阻 $ R_{2} $是由超导体材料制成的
B.检测的气体酒精浓度越小,电压表的示数越小
C.检测的气体酒精浓度越大,$ R_{2} $的阻值越大
D.检测的气体酒精浓度越大,电路中的电流越小
答案:
B
查看更多完整答案,请扫码查看


