《2025年超能学典计算加解决问题六年级数学上册苏教版》

1 直接写得数。
$8× \frac {3}{4}= $
$\frac {6}{7}÷3= $
$\frac {1}{5}+\frac {1}{6}= $
$\frac {10}{9}×\frac {3}{5}= $
$\frac {2}{5}÷\frac {2}{5}= $
$\frac {1}{3}×\frac {1}{4}= $
$16÷\frac {4}{9}= $
$\frac {1}{2}-\frac {3}{8}= $
$\frac {1}{4}-\frac {1}{5}= $
$\frac {3}{10}×0= $
$\frac {7}{16}÷\frac {7}{8}= $
$\frac {1}{2}×\frac {3}{4}÷\frac {1}{2}×\frac {3}{4}= $

答案： 1. 6 $\frac{2}{7}$ $\frac{11}{30}$ $\frac{2}{3}$ 1 $\frac{1}{12}$ 36 $\frac{1}{8}$ $\frac{1}{20}$ 0 $\frac{1}{2}$ $\frac{9}{16}$

2 在〇里填“＞”“＜”或“=”。
$\frac {4}{3}×\frac {8}{9}◯\frac {4}{3}$
$\frac {11}{9}÷\frac {4}{3}◯\frac {11}{9}$
$\frac {1}{2}÷\frac {3}{5}◯\frac {1}{2}$
$1.2÷\frac {2}{5}◯1.2×\frac {2}{5}$
$14×\frac {5}{6}◯14$
$\frac {4}{9}×\frac {1}{4}◯\frac {9}{4}×\frac {1}{4}$

答案： 2. ＜ ＜ ＞ ＞ ＜ ＜

1 (基础题)

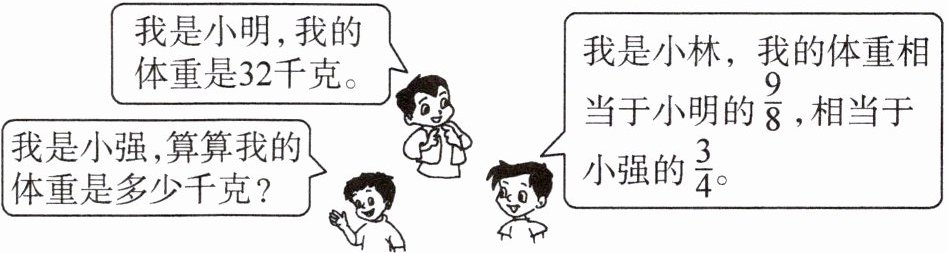
答案： 1. $32×\frac{9}{8}÷\frac{3}{4}=$48(千克)

2 (重点题)甲、乙、丙三人钱数的比是$2:4:5$。已知乙、丙二人钱数的和是171元,甲有多少元?

答案： 2. $171÷(4+5)=19$(元)$19×2=38$(元)

3 (拓展题)球从高空落下,弹起的高度约是落下高度的$\frac {2}{5}$。如果球从25米的高空落下,弹起后再落下,那么至少弹起几次后它的弹起高度不足0.5米?

答案： 3. $25×\frac{2}{5}×\frac{2}{5}×\frac{2}{5}×\frac{2}{5}=\frac{16}{25}$(米) $\frac{16}{25}＞\frac{1}{2}$ $\frac{16}{25}×\frac{2}{5}=\frac{32}{125}$(米)$\frac{32}{125}＜\frac{1}{2}$ 至少弹起5次后它的弹起高度不足0.5米 提示:算出每一次弹起的高度与$\frac{1}{2}$进行比较。