在课本第8页“分割三角形”的问题中,第100次操作后得到的图形中涂色三角形的个数为
$1+3+3^{2}+3^{3}+\cdots +3^{99}$
(列出算式,不用计算)。
答案:
$1+3+3^{2}+3^{3}+\cdots +3^{99}$
1. (2024·徐州)观察下列各数:3,8,18,38,…按此规律,第5~7个数可能为(
A.48,58,68
B.58,78,98
C.76,156,316
D.78,158,318
D
)A.48,58,68
B.58,78,98
C.76,156,316
D.78,158,318
答案:
D
2. (新情境·游戏活动)(2024·哈尔滨)如图,用棋子摆出一组形如正方形的图形,按照这种方法摆下去,摆第⑤个图形需要棋子(
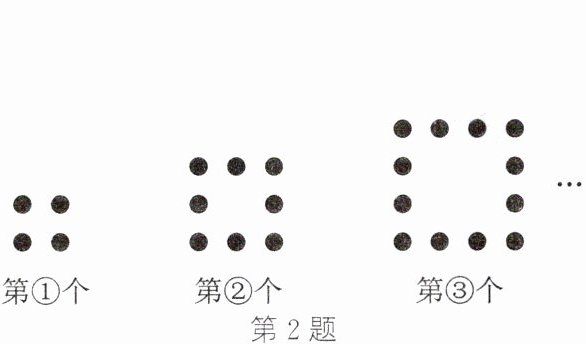
A.16枚
B.20枚
C.24枚
D.25枚
B
)
A.16枚
B.20枚
C.24枚
D.25枚
答案:
B
3. (2023·常德)观察如图所示的数表(横排为行,竖排为列),按数表中的规律,分数$\frac {20}{2023}$若排在第a行,第b列,则$a - b$的值为

2022
。
答案:
2022 解析:观察数表,可得同一行的分数,分子与分母的和不变,且$\frac{n}{m}$(m,n 为正整数)在第(m+n-1)行,第 n列,所以$\frac{20}{2023}$在第 2042 行,第 20 列,则a=2042,b=20.所以a-b=2042-20=2022.
4. (新考法·综合与实践)(2023·枣庄)
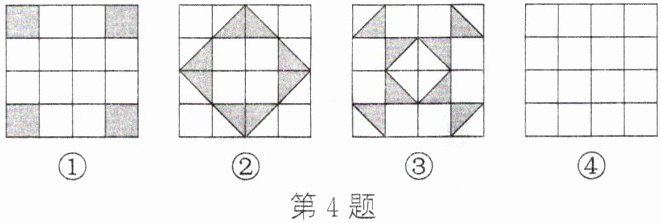
(1) 观察分析:在一次数学综合实践活动中,老师向同学们展示了图①,图②,图③三幅图形,观察图中涂色部分构成的图案,请写出两个这三个图案的共同特征;
(2) 动手操作:请在图④中设计一个新的图案,使其满足你在(1)中发现的共同特征。
(1) 观察分析:在一次数学综合实践活动中,老师向同学们展示了图①,图②,图③三幅图形,观察图中涂色部分构成的图案,请写出两个这三个图案的共同特征;
(2) 动手操作:请在图④中设计一个新的图案,使其满足你在(1)中发现的共同特征。

答案:
答案不唯一,如
(1)① 沿一条直线翻折后,图案两侧可以重合 ② 涂色部分的面积之和相等 (2)如图所示

答案不唯一,如
(1)① 沿一条直线翻折后,图案两侧可以重合 ② 涂色部分的面积之和相等 (2)如图所示

查看更多完整答案,请扫码查看


