1. 表示
相等
关系的式子叫作等式。
答案:
相等
2. 等式的基本性质1:等式两边都加上(或减去)同一个
数
或整式
,所得结果仍是等式。用字母可以表示为:如果$a = b$,那么$a\pm m= $$b\pm m$
。
答案:
数 整式 $b\pm m$
3. 等式的基本性质2:等式两边都乘(或除以)同一个
数(除数不能为0)
,所得结果仍是等式。用字母可以表示为:(1)如果$a = b$,那么$am=$$bm$
;(2)如果$a = b$,且$m\neq0$,那么$\frac{a}{m}$
$=\frac{b}{m}$。
答案:
数(除数不能为0) (1)$bm$ (2)$\frac{a}{m}$
1. 已知$a = b$,下列等式不一定成立的是(
A.$a + 1 = b + 1$
B.$2a = b + 2$
C.$2a = 2b$
D.$a - b = 0$
B
)A.$a + 1 = b + 1$
B.$2a = b + 2$
C.$2a = 2b$
D.$a - b = 0$
答案:
B
2. 在等式$2x + 5 = 9$的两边都
减去5
,得$2x = 9-$______5
。
答案:
减去5 5
3. 由$3(a + 1)x = 4(a + 1)$得到$3x = 4$成立的限制条件是
$a\neq -1$
。
答案:
$a\neq -1$
4. (新考法·新定义题)规定:若$a - b = 0$,则称$a与b$互为“天平数”。若$3x^{2}-5与-x + 4$互为“天平数”,则代数式$9x^{2}+3x - 7$的值为
20
。
答案:
20 解析:根据题意,得$3x^{2}-5-(-x+4)=0$.化简,得$3x^{2}+x-9=0$.利用等式的基本性质1,得$3x^{2}+x=9$.所以$9x^{2}+3x-7=3(3x^{2}+x)-7=3× 9-7=20$.
5. 根据下面情景中的等量关系列出一个等式:
(1)如图,一个长方形纸片被分割成四部分。
(2)(2023·呼伦贝尔改编)某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分。某队在12场比赛中胜$x$场,得20分。
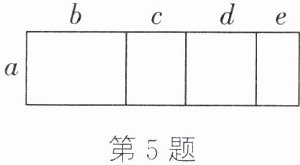
(1)如图,一个长方形纸片被分割成四部分。
(2)(2023·呼伦贝尔改编)某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分。某队在12场比赛中胜$x$场,得20分。

答案:
(1)$a(b+c+d+e)=ab+ac+ad+ae$ (2)$2x+12-x=20$
6. 利用等式的基本性质,将下列等式变形为$x = c$($c$为常数)的形式:
(1)$x + 7 = 10$;
(2)$-\frac{1}{3}x = 3$;
(3)$3x + 2 = x - 6$。
(1)$x + 7 = 10$;
(2)$-\frac{1}{3}x = 3$;
(3)$3x + 2 = x - 6$。
答案:
(1)$x=3$ (2)$x=-9$ (3)$x=-4$
查看更多完整答案,请扫码查看


