《2025年亮点给力大试卷八年级物理上册苏科版》

25. (10分)如图所示是“测量小车沿斜面下滑的平均速度”的实验装置.

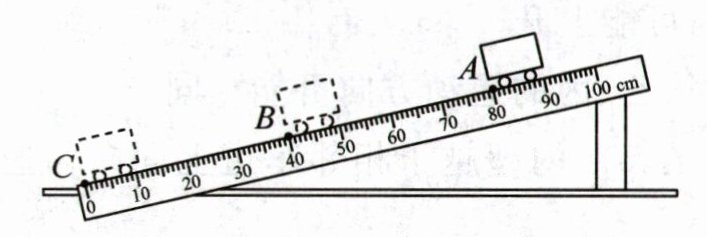
(1) 该实验的原理是$v=\frac{s}{t}$(填公式).
(2) 应使斜面保持较小(选填“较大”或“较小”)的坡度,以减小测量时间的误差.
(3) 小车从A点运动到C点,运动的路程是80.0cm.如果让小车过了A点才开始计时,则所测得AC段的平均速度与实际相比偏大(选填“偏大”“偏小”或“无影响”).
(4) 实验中,关于如何得到下半程s_{BC}的平均速度v_{BC},下列方法最好的是C.
A. 小车从B点由静止释放,测出B点到C点所用时间t_{BC}与路程s_{BC},计算得到v_{BC}
B. 小车从A点由静止释放,经过B点开始计时,到达C点后测得时间t_{BC},再测量路程s_{BC},计算得到v_{BC}
C. 不测量,利用已有数据求得t_{BC}= t_{AC}-t_{AB}、s_{BC}= s_{AC}-s_{AB},再计算得到v_{BC}
(5) 如上表是实验时设计的数据记录表格,则“?”一栏里应填写的内容是平均速度$v/(m·s^{-1})$.

答案：
(1)$v=\frac{s}{t}$　
(2)较小　时间　
(3)80.0　偏大　
(4)C　
(5)平均速度$v/(m·s^{-1})$

26. (12分)(2025·江苏扬州期末)课外实践活动中,小明用秒表和刻度尺测量纸锥下落的速度.
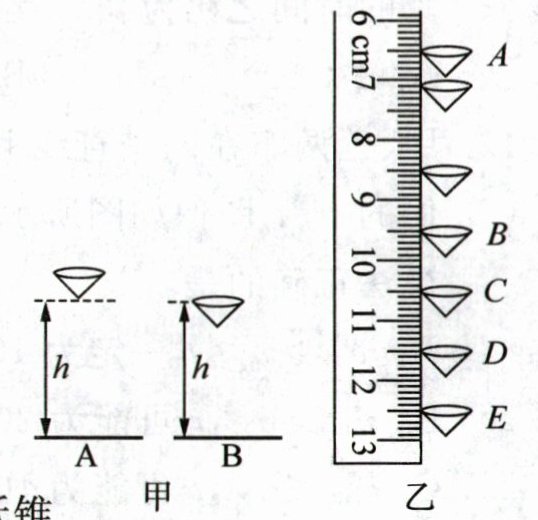
(1) 对于纸锥下落前的初始位置有如图甲所示的A、B两种摆放方式,你认为正确的是A.

(2) 小明用秒表分别测出三次纸锥下落的时间,然后算出其下落的平均速度,下面两种处理方法,你认为合理的是A.
A. 算出三次时间的平均值,从而得出纸锥下落的平均速度
B. 分别算出三次下落的速度,从而得出纸锥下落的平均速度
(3) 为了更加准确地测出纸锥下落的速度,小明用频闪相机拍摄纸锥下落的照片,并用刻度尺测出纸锥间的距离,如图乙.
① 由图乙可知,该纸锥下落过程速度的变化情况是先变大后不变;
② 已知相机每隔0.2s拍摄一次,照片中A、E间的距离与纸锥实际下落的距离之比为1:20,则纸锥经过C位置时的速度为1m/s.
(4) 实验结束后,小明思考纸锥下落的快慢与哪些因素有关呢? 他认为与材料有关,因为相同形状的纸锥越重,空气阻力的影响越小,下落得越快.你认为还与什么有关? 锥角的大小,理由是其他条件一定时，锥角越大，受到的空气阻力越大，下落越慢.

答案：
(1)A　
(2)A　
(3)①先变大后不变　1　
(4)锥角的大小　其他条件一定时，锥角越大，受到的空气阻力越大，下落越慢
解析:
(1)实验中记录纸锥下落时间是从纸锥释放到纸锥下端触地的时间，所以纸锥下落高度应为纸锥下端移动的距离，故两种摆放方式中A是正确的。
(2)实验中纸锥下落高度一定，而受空气阻力、释放时纸锥轴线是否竖直等因素的影响，纸锥在空气中运动时间的测量误差会较大，算出三次时间的平均值，可减小测量时间的误差，这样得出纸锥下落的平均速度误差相对较小。若分别算出三次下落的速度，相当于放大了误差，再计算纸锥下落的平均速度误差相对较大。故A更合理。
(3)①由图乙可知，纸锥在下落过程中，在相同时间内下落路程先变大后不变，由$v=\frac{s}{t}$可知，纸锥的速度先变大后不变。②由图乙可知，纸锥在下落过程中，在相同时间内下落路程先变大后不变，由$v=\frac{s}{t}$可知，纸锥的速度先变大后不变。②由图乙可知，纸锥在B到E位置之间，相同时间间隔内通过的距离相同，做的是匀速直线运动。图中刻度尺分度值为1mm，BE之间的距离为12.90cm - 9.90cm=3.00cm，由于照片上距离与实际距离的比值为1:20，所以BE间的实际距离为3.00cm×20=60.00cm，纸锥经过B、E两点所用的时间为0.2s×3=0.6s。由于纸锥在BE之间做匀速直线运动，所以纸锥在C位置时的速度等于在BE之间的速度$v=\frac{s}{t}=\frac{60.00×10^{-2}m}{0.6s}=1m/s$。
(4)纸锥下落速度可能与锥角大小有关。因为其他条件一定时，锥角越大，受到的空气阻力越大，下落越慢。