19. (6分)将第一行的图形绕轴旋转一周,便得到第二行的几何体,用线连一连:


答案:
如图所示.

如图所示.

20. (6分)如图所示,由直角三角形和正方形拼成的四边形.
(1)将这个四边形绕图中虚线旋转一周,可以得到一个立体图形,这能说明的事实是______.(选择正确的一项序号)
①点动成线;②线动成面;③面动成体.
(2)求得到的立体图形的体积. ($V_{圆柱}= πr^{2}h$,$V_{圆锥}= \frac{1}{3}πr^{2}h$,r为圆柱和圆锥底面半径,h为圆柱和圆锥的高,结果保留π)

(1)将这个四边形绕图中虚线旋转一周,可以得到一个立体图形,这能说明的事实是______.(选择正确的一项序号)
①点动成线;②线动成面;③面动成体.
(2)求得到的立体图形的体积. ($V_{圆柱}= πr^{2}h$,$V_{圆锥}= \frac{1}{3}πr^{2}h$,r为圆柱和圆锥底面半径,h为圆柱和圆锥的高,结果保留π)

答案:
(1)③ [解析]
∵四边形是平面图形,绕图中虚线旋转一周,可以得到一个立体图形,
∴是面动成体.
(2)
∵V圆柱=πr²h=π×3²×5=45π,V圆锥=1/3πr²h=1/3×π×3²×2=6π,
∴V=V圆柱 - V圆锥=45π - 6π=39π.
(1)③ [解析]
∵四边形是平面图形,绕图中虚线旋转一周,可以得到一个立体图形,
∴是面动成体.
(2)
∵V圆柱=πr²h=π×3²×5=45π,V圆锥=1/3πr²h=1/3×π×3²×2=6π,
∴V=V圆柱 - V圆锥=45π - 6π=39π.
21. (8分)(2025·重庆南岸区期末)如图(1)所示,是由一些大小相同的边长为10cm的小立方块搭成的几何体从上面看到的图形,其中小正方形中的数字表示该位置上的小立方块的个数.
(1)请在图(2)相应的方格内,画出从正面看和从左面看,得到的该几何体的形状图;
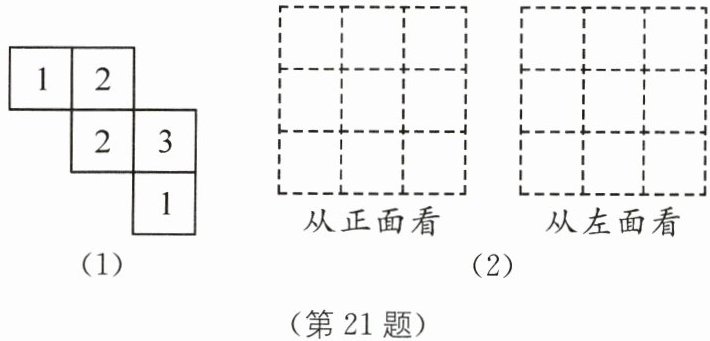
(2)求这个几何体的表面积.
(1)请在图(2)相应的方格内,画出从正面看和从左面看,得到的该几何体的形状图;

(2)求这个几何体的表面积.
答案:
(1)如图所示:

(2)该几何体的表面积为2×(6+6+5)×10×10=3400(cm²).
(1)如图所示:

(2)该几何体的表面积为2×(6+6+5)×10×10=3400(cm²).
查看更多完整答案,请扫码查看


