《2025年课时训练七年级数学上册苏科版江苏人民出版社》

8. 如图,正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开,外表面朝上,展开图可能是( ).

答案： B

9. 如图是一个长方体纸盒的展开图,在展开图的每一个面上都标有数字,如果折叠成长方体纸盒后,标有数字“1”的面是纸盒的底部,那么它最上面的面的数字为______.

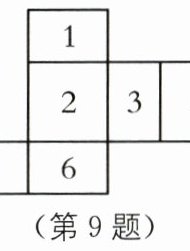
答案： 6

10. 如图,三组图形都是由四个等边三角形组成,能折成多面体的选项序号是______.

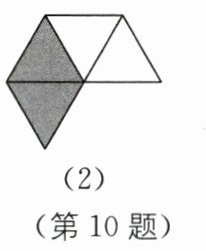
答案：
(1)
(3)

11. (2025·陕西西安期末)如图,将三角形绕虚线旋转一周得到的几何体是______.

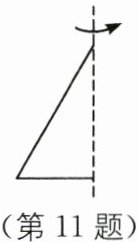
答案： 圆锥

12. 如图是一个五棱柱,用平面将其截成两个几何体,若其中一个几何体为三棱柱,则另一个几何体最少有______个面.

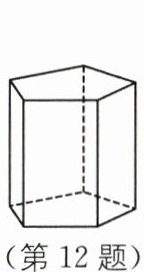
答案： 6

13. 若用平面分别截下列几何体:①三棱柱;②三棱锥;③正方体;④圆锥;⑤球,得到的截面不可能是三角形的是______.(填写正确的几何体前的序号)

答案： ⑤

14. (2025·河南鹤壁期末)如图所示,这是一个正方体的表面展开图,正方体中相对的面上的数字或代数式互为相反数,则y的值为______.

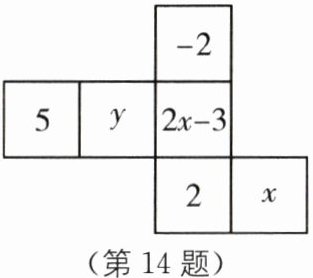
答案： 1

15. 将一个长方体的一个角切去,所得的立体图形的棱的数量为______.

答案：
12条或13条或14条或15条 [解析]根据题意分为以下四种情况讨论:
注意分情况讨论

①如图
(1),12+3=15(条);
②如图
(2),12 - 1+3=11+3=14(条);
③如图
(3),12 - 3+3=9+3=12(条);
④如图
(4),12 - 2+3=10+3=13(条).
综上所述,所得立体图形的棱的条数为15条或14条或13条或12条.
解题关键 本题考查了长方体的特征和截长方体,明确在顶点处截去一个角就多出3条棱是解题关键.

16. 用一个平面截一个直n棱柱,得到的截面边数最多是8条,且这个n棱柱的每个侧面都是正方形,正方形的面积为4,则这个n棱柱的棱长之和为______.

答案： 36

17. 十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式:$V + F - E = 2$,被称为欧拉公式.若一个多面体的面数比顶点数少8,且有30条棱,则这个多面体的顶点数是______.

答案： 20

18. 有一个正六面体骰(tóu)子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动$90^{\circ}$算一次,则滚动第2024次后,骰子朝下一面的点数是______.

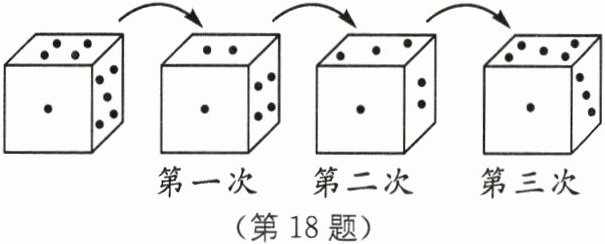
答案： 3 [解析]观察图形知道点数3和点数4相对,点数2和点数5相对.
∵2024÷4=506,
∴滚动第2024次后与第四次相同,
四次一循环
∴朝下的数字是4的对面3.

22. (8分)如图是一个长方体的表面展开图,一共标有A,B,C,D,E,F六个面,$MN = 2$,$NO = x$,$OP = y$.请根据要求回答:
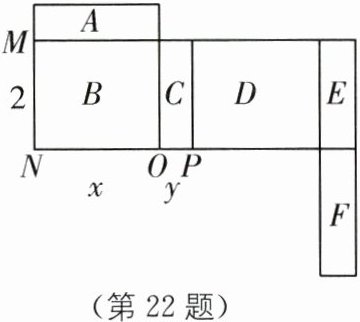
(1)如果A面在长方体的底部,那么______面会在上面;
(2)求这个长方体的表面积和体积;(用含x和y的式子表示)
(3)若$A = a^{3}+\frac{1}{2}a^{2}b + 3$,$B = \frac{1}{2}a^{2}b - 3$,$C = a^{3} - 1$,$D = -\frac{1}{2}(a^{2}b - 6)$,且相对两个面上式子的和都相等,求E代表的代数式.

答案：
(1)F
(2)由题意可知这个长方体的长x、宽为y、高为2,因此表面积为(xy+2x+2y)×2=2xy+4x+4y,体积为2xy.
(3)由题意可知B+D=C+E,
所以E=B+D - C=(1/2a²b - 3)-1/2(a²b - 6)-(a³ - 1)=1/2a²b - 3 - 1/2a²b+3 - a³+1=1 - a³,
即E所代表的代数式为1 - a³.