《2025年暑假作业完美假期生活八年级数学湖南教育出版社》

7. 对于一次函数$y = - 2x + 4$，下列结论正确的有（C）
①函数的图象不经过第三象限；
②函数的图象与x轴的交点坐标是$(2,0)$；
③函数的图象向下平移4个单位长度得$y = - 2x$的图象；
④若两点$A(1,y_{1})$，$B(3,y_{2})$，在该函数图象上，则$y_{1} ＜ y_{2}$.
A. 1个
B. 2个
C. 3个
D. 4个

答案： C

8. 下列命题是真命题的是（D）
A. 同位角相等
B. 若$ax ＞ a$，则$x ＞ 1$
C. 若$|a| = |b|$，则$a = b$
D. 若$m = n$，则$m^{2} = n^{2}$

答案： D

9. 二次根式$\sqrt{x - 3}$有意义的条件是（D）
A. $x ＞ 3$
B. $x ＞ - 3$
C. $x \geqslant - 3$
D. $x \geqslant 3$

答案： D

10. 当$2 \leqslant x \leqslant 5$时，一次函数$y = (m + 1)x + m^{2} + 1$有最大值6，则实数m的值为（A）
A. -3或0
B. 0或1
C. -5或-3
D. -5或1

答案： A

11. 若直线$y = kx - 6$与坐标轴围成的三角形的面积为9，则$k = $$\pm 2$.

答案： $\pm 2$

12. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，则小正方形的面积为____（用a，b表示代数式）

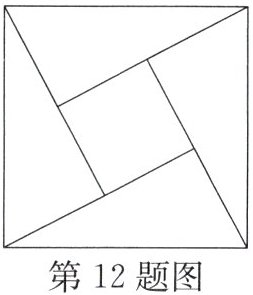
12. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，则小正方形的面积为__$(a - b)^2$__（用a，b表示代数式）

答案： $(a - b)^2$

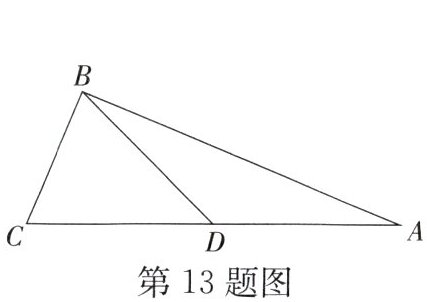
13. 如图，在$Rt\triangle ABC$中，$\angle ABC = 90^{\circ}$，$BC = 5$，D为AC中点，连接BD，$BD = \frac{13}{2}$，则线段AB的长度为12.

答案： 12

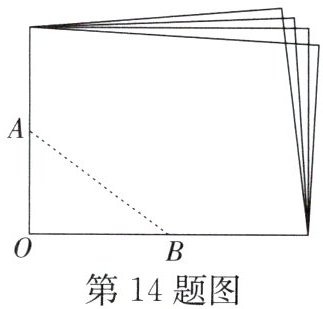
14. 如图，将一张矩形纸片对折再对折，然后沿图中的虚线AB剪下，已知$AB = 5$，$OA = 3$，再将剪下的纸片展开，则得到一个新的四边形，它的面积是____.

14. 如图，将一张矩形纸片对折再对折，然后沿图中的虚线AB剪下，已知$AB = 5$，$OA = 3$，再将剪下的纸片展开，则得到一个新的四边形，它的面积是24.

答案： 24