2025年暑假作业完美假期生活八年级数学湖南教育出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业完美假期生活八年级数学湖南教育出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
13. 如图,正方形$ABCD$中,$E$是$BC$延长线上一点,在$AB$上取一点$F$,使点$B$关于直线$EF$的对称点$G$落在$AD$上,连接$EG$交于$H$,连接$BH$交$EF$于$I$. 连接$CI$,则下列结论,①$∠1 = ∠2$;②$∠3 = ∠GBH$;③$GD = \sqrt{3}GI$;④若$AG = 1$,$GD = 2$,则$BI = \sqrt{5}$. 其中正确的是____
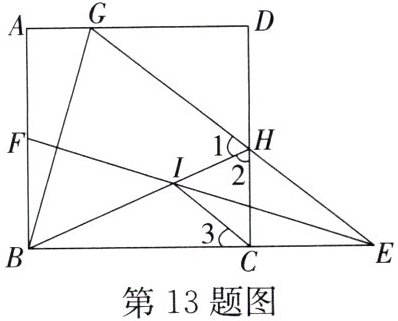
①②④
. (填序号)
答案:
①②④
14. 若一次函数$y = kx - x + 3k - 2$的图象经过第一、二、四象限,则实数$k$的取值范围为____
$\frac{2}{3} < k < 1$
.
答案:
$\frac{2}{3} < k < 1$
15. 如图,在矩形$ABCD$中,$AB = 3$,$BC = 1 + 2\sqrt{3}$,$E$为$BC$上一点,且$BE = 1$,$F$为$AB$上一个动点,连接$EF$,将$EF$绕点$E$顺时针旋转$30^{\circ}$到$EG$位置,连接$FG$和$CG$,则$CG$的最小值为__
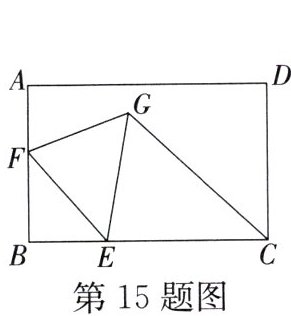
4
__.
答案:
4
16. 已知$y + 2$与$2x - 3$成正比例,且当$x = 3$时,$y = 1$,求$y$与$x$之间的函数表达式为
$y = 2x - 5$
.
答案:
$y = 2x - 5$
17. 如图,在$\triangle ABC$中,$∠ACB = 90^{\circ}$,点$D$是$AB$的中点,过点$D$作$DE \perp AC$于点$E$,延长$DE$到点$F$,使得$EF = DE$,连接$AF$,$CF$.
(1)根据题意,补全图形;
(2)求证:四边形$ADCF$是菱形;
(3)若$AB = 8$,$∠BAC = 30^{\circ}$,求$\triangle ABC$的面积.
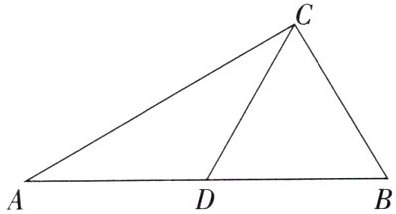
(1)根据题意,补全图形;
(2)求证:四边形$ADCF$是菱形;
(3)若$AB = 8$,$∠BAC = 30^{\circ}$,求$\triangle ABC$的面积.

答案:
(1)如图所示:

(2)证明:因为 D 是 AB 的中点,$∠ACB = 90^{\circ}$,所以 $AD = CD = \frac{1}{2}AB$,因为 $DE⊥AC$,所以 $AE = CE$,因为 $ED = EF$,所以四边形 ADCF 是平行四边形,因为 $AC⊥DF$,所以四边形 ADCF 是菱形. (3)$8\sqrt{3}$
(1)如图所示:

(2)证明:因为 D 是 AB 的中点,$∠ACB = 90^{\circ}$,所以 $AD = CD = \frac{1}{2}AB$,因为 $DE⊥AC$,所以 $AE = CE$,因为 $ED = EF$,所以四边形 ADCF 是平行四边形,因为 $AC⊥DF$,所以四边形 ADCF 是菱形. (3)$8\sqrt{3}$
查看更多完整答案,请扫码查看


