2025年暑假作业完美假期生活八年级数学湖南教育出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业完美假期生活八年级数学湖南教育出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 在直角三角形中,有一个锐角为52°,那么另一个锐角的度数为
$ 38^{\circ} $
.
答案:
$ 38^{\circ} $
8. 在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为
4
。
答案:
4
9. 如图,AF=DC,BC//FE,只需补充一个条件____
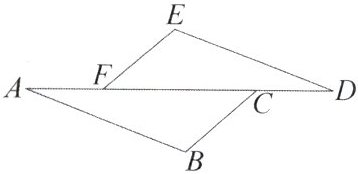
$ BC = EF $
____,就可得△ABC≌△DEF.
答案:
$ BC = EF $
10. △ABC中,AB=AC=6,∠B=30°,则BC边上的高AD=
3
.
答案:
3
11. 如图,在△ABC中,已知∠ACB=90°,CD,CE三等分∠ACB,CD⊥AB.
求证:(1)在$Rt\triangle ABC$中,$\angle A = 30^{\circ}$,根据直角三角形性质得$BC=\frac{1}{2}AB$,即
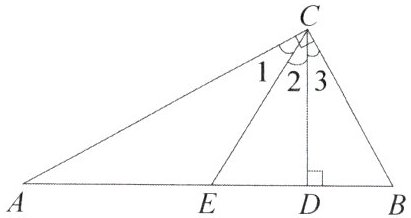
求证:(1)在$Rt\triangle ABC$中,$\angle A = 30^{\circ}$,根据直角三角形性质得$BC=\frac{1}{2}AB$,即
$AB = 2BC$
;(2)由$\angle A=\angle1$得$AE = CE$,$\triangle BCE$是等边三角形得$CE = EB$,所以$CE = AE = EB$
.
答案:
【解析】:
### (1)证明$AB = 2BC$
已知$\angle ACB = 90^{\circ}$,$CD$,$CE$三等分$\angle ACB$,则$\angle1=\angle2=\angle3 = 30^{\circ}$。
因为$CD\perp AB$,$\angle3 = 30^{\circ}$,在$Rt\triangle BCD$中,$\angle B = 60^{\circ}$。
在$Rt\triangle ABC$中,$\angle A=180^{\circ}-\angle ACB - \angle B=180^{\circ}-90^{\circ}-60^{\circ}=30^{\circ}$。
根据直角三角形中$30^{\circ}$所对的直角边等于斜边的一半,在$Rt\triangle ABC$中,$\angle A = 30^{\circ}$,所以$BC=\frac{1}{2}AB$,即$AB = 2BC$。
### (2)证明$CE = AE = EB$
由(1)知$\angle A = 30^{\circ}$,$\angle1 = 30^{\circ}$,所以$\angle A=\angle1$,根据等角对等边,可得$AE = CE$。
又因为$\angle B = 60^{\circ}$,$\angle2+\angle3=60^{\circ}$,即$\angle BCE = 60^{\circ}$,所以$\triangle BCE$是等边三角形(有一个角是$60^{\circ}$的等腰三角形是等边三角形,$\angle B = 60^{\circ}$,$CE = BC$),则$CE = EB$。
综上,$CE = AE = EB$。
【答案】:
(1)在$Rt\triangle ABC$中,$\angle A = 30^{\circ}$,根据直角三角形性质得$BC=\frac{1}{2}AB$,即$\boldsymbol{AB = 2BC}$。
(2)由$\angle A=\angle1$得$AE = CE$,$\triangle BCE$是等边三角形得$CE = EB$,所以$\boldsymbol{CE = AE = EB}$。
### (1)证明$AB = 2BC$
已知$\angle ACB = 90^{\circ}$,$CD$,$CE$三等分$\angle ACB$,则$\angle1=\angle2=\angle3 = 30^{\circ}$。
因为$CD\perp AB$,$\angle3 = 30^{\circ}$,在$Rt\triangle BCD$中,$\angle B = 60^{\circ}$。
在$Rt\triangle ABC$中,$\angle A=180^{\circ}-\angle ACB - \angle B=180^{\circ}-90^{\circ}-60^{\circ}=30^{\circ}$。
根据直角三角形中$30^{\circ}$所对的直角边等于斜边的一半,在$Rt\triangle ABC$中,$\angle A = 30^{\circ}$,所以$BC=\frac{1}{2}AB$,即$AB = 2BC$。
### (2)证明$CE = AE = EB$
由(1)知$\angle A = 30^{\circ}$,$\angle1 = 30^{\circ}$,所以$\angle A=\angle1$,根据等角对等边,可得$AE = CE$。
又因为$\angle B = 60^{\circ}$,$\angle2+\angle3=60^{\circ}$,即$\angle BCE = 60^{\circ}$,所以$\triangle BCE$是等边三角形(有一个角是$60^{\circ}$的等腰三角形是等边三角形,$\angle B = 60^{\circ}$,$CE = BC$),则$CE = EB$。
综上,$CE = AE = EB$。
【答案】:
(1)在$Rt\triangle ABC$中,$\angle A = 30^{\circ}$,根据直角三角形性质得$BC=\frac{1}{2}AB$,即$\boldsymbol{AB = 2BC}$。
(2)由$\angle A=\angle1$得$AE = CE$,$\triangle BCE$是等边三角形得$CE = EB$,所以$\boldsymbol{CE = AE = EB}$。
12. 已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为点E. 求证:AD=AE.
证明:
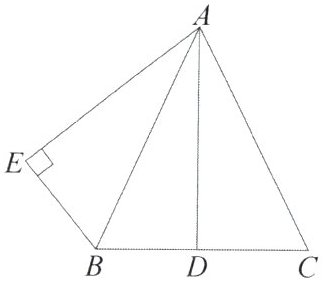
证明:
$ \because AB = AC $,点 $ D $ 是 $ BC $ 的中点,$ \therefore \angle ADB = 90^{\circ} $。$ \because AE \perp EB $,$ \therefore \angle E = \angle ADB = 90^{\circ} $,$ \because AB $ 平分 $ \angle DAE $,$ \therefore \angle BAD = \angle BAE $。在 $ \triangle ADB $ 和 $ \triangle AEB $ 中,$ \angle E = \angle ADB = 90^{\circ} $,$ \angle BAD = \angle BAE $,$ AB = AB $,$ \therefore \triangle ADB \cong \triangle AEB (AAS) $,$ \therefore AD = AE $。

答案:
证明:$ \because AB = AC $,点 $ D $ 是 $ BC $ 的中点,$ \therefore \angle ADB = 90^{\circ} $。$ \because AE \perp EB $,$ \therefore \angle E = \angle ADB = 90^{\circ} $,$ \because AB $ 平分 $ \angle DAE $,$ \therefore \angle BAD = \angle BAE $。在 $ \triangle ADB $ 和 $ \triangle AEB $ 中,$ \angle E = \angle ADB = 90^{\circ} $,$ \angle BAD = \angle BAE $,$ AB = AB $,$ \therefore \triangle ADB \cong \triangle AEB (AAS) $,$ \therefore AD = AE $。
13. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°. 求:
(1)∠BAE的度数.
解:$ \because \angle B + \angle C + \angle BAC = 180^{\circ} $,$ \therefore \angle BAC = 180^{\circ} - \angle B - \angle C = 180^{\circ} - 70^{\circ} - 30^{\circ} = 80^{\circ} $。$ \because AE $ 平分 $ \angle BAC $,$ \therefore \angle BAE = \frac{1}{2} \angle BAC = $
(2)∠DAE的度数.
解:$ \because AD \perp BC $,$ \therefore \angle ADE = 90^{\circ} $,而 $ \angle ADE = \angle B + \angle BAD $,$ \therefore \angle BAD = 90^{\circ} - \angle B = 90^{\circ} - 70^{\circ} = 20^{\circ} $,$ \therefore \angle DAE = \angle BAE - \angle BAD = 40^{\circ} - 20^{\circ} = $
(3)探究:亮亮认为如果条件∠B=70°,∠C=30°改成∠B−∠C=40°,也能得出∠DAE的度数. 你认为能吗?若能,请你写出求解过程;若不能,请说明理由.
解:能。$ \because \angle B + \angle C + \angle BAC = 180^{\circ} $,$ \therefore \angle BAC = 180^{\circ} - \angle B - \angle C $。$ \because AE $ 平分 $ \angle BAC $,$ \therefore \angle BAE = \frac{1}{2} \angle BAC = \frac{1}{2} (180^{\circ} - \angle B - \angle C) = 90^{\circ} - \frac{1}{2} (\angle B + \angle C) $。$ \because AD \perp BC $,$ \therefore \angle ADE = 90^{\circ} $,而 $ \angle ADE = \angle B + \angle BAD $,$ \therefore \angle BAD = 90^{\circ} - \angle B $,$ \therefore \angle DAE = \angle BAE - \angle BAD = 90^{\circ} - \frac{1}{2} (\angle B + \angle C) - (90^{\circ} - \angle B) = \frac{1}{2} (\angle B - \angle C) $。$ \because \angle B - \angle C = 40^{\circ} $,$ \therefore \angle DAE = \frac{1}{2} × 40^{\circ} = $
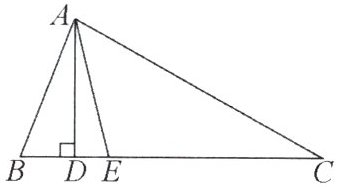
(1)∠BAE的度数.
解:$ \because \angle B + \angle C + \angle BAC = 180^{\circ} $,$ \therefore \angle BAC = 180^{\circ} - \angle B - \angle C = 180^{\circ} - 70^{\circ} - 30^{\circ} = 80^{\circ} $。$ \because AE $ 平分 $ \angle BAC $,$ \therefore \angle BAE = \frac{1}{2} \angle BAC = $
$40^{\circ}$
。(2)∠DAE的度数.
解:$ \because AD \perp BC $,$ \therefore \angle ADE = 90^{\circ} $,而 $ \angle ADE = \angle B + \angle BAD $,$ \therefore \angle BAD = 90^{\circ} - \angle B = 90^{\circ} - 70^{\circ} = 20^{\circ} $,$ \therefore \angle DAE = \angle BAE - \angle BAD = 40^{\circ} - 20^{\circ} = $
$20^{\circ}$
。(3)探究:亮亮认为如果条件∠B=70°,∠C=30°改成∠B−∠C=40°,也能得出∠DAE的度数. 你认为能吗?若能,请你写出求解过程;若不能,请说明理由.
解:能。$ \because \angle B + \angle C + \angle BAC = 180^{\circ} $,$ \therefore \angle BAC = 180^{\circ} - \angle B - \angle C $。$ \because AE $ 平分 $ \angle BAC $,$ \therefore \angle BAE = \frac{1}{2} \angle BAC = \frac{1}{2} (180^{\circ} - \angle B - \angle C) = 90^{\circ} - \frac{1}{2} (\angle B + \angle C) $。$ \because AD \perp BC $,$ \therefore \angle ADE = 90^{\circ} $,而 $ \angle ADE = \angle B + \angle BAD $,$ \therefore \angle BAD = 90^{\circ} - \angle B $,$ \therefore \angle DAE = \angle BAE - \angle BAD = 90^{\circ} - \frac{1}{2} (\angle B + \angle C) - (90^{\circ} - \angle B) = \frac{1}{2} (\angle B - \angle C) $。$ \because \angle B - \angle C = 40^{\circ} $,$ \therefore \angle DAE = \frac{1}{2} × 40^{\circ} = $
$20^{\circ}$
。
答案:
解:(1)$ \because \angle B + \angle C + \angle BAC = 180^{\circ} $,$ \therefore \angle BAC = 180^{\circ} - \angle B - \angle C = 180^{\circ} - 70^{\circ} - 30^{\circ} = 80^{\circ} $。$ \because AE $ 平分 $ \angle BAC $,$ \therefore \angle BAE = \frac{1}{2} \angle BAC = 40^{\circ} $。(2)$ \because AD \perp BC $,$ \therefore \angle ADE = 90^{\circ} $,而 $ \angle ADE = \angle B + \angle BAD $,$ \therefore \angle BAD = 90^{\circ} - \angle B = 90^{\circ} - 70^{\circ} = 20^{\circ} $,$ \therefore \angle DAE = \angle BAE - \angle BAD = 40^{\circ} - 20^{\circ} = 20^{\circ} $。(3)能。$ \because \angle B + \angle C + \angle BAC = 180^{\circ} $,$ \therefore \angle BAC = 180^{\circ} - \angle B - \angle C $。$ \because AE $ 平分 $ \angle BAC $,$ \therefore \angle BAE = \frac{1}{2} \angle BAC = \frac{1}{2} (180^{\circ} - \angle B - \angle C) = 90^{\circ} - \frac{1}{2} (\angle B + \angle C) $。$ \because AD \perp BC $,$ \therefore \angle ADE = 90^{\circ} $,而 $ \angle ADE = \angle B + \angle BAD $,$ \therefore \angle BAD = 90^{\circ} - \angle B $,$ \therefore \angle DAE = \angle BAE - \angle BAD = 90^{\circ} - \frac{1}{2} (\angle B + \angle C) - (90^{\circ} - \angle B) = \frac{1}{2} (\angle B - \angle C) $。$ \because \angle B - \angle C = 40^{\circ} $,$ \therefore \angle DAE = \frac{1}{2} × 40^{\circ} = 20^{\circ} $。
查看更多完整答案,请扫码查看


