2025年暑假作业完美假期生活八年级数学湖南教育出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业完美假期生活八年级数学湖南教育出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 顺次连接四边形各边中点所得的四边形是
平行四边形
。
答案:
平行四边形
8. $\triangle ABC$ 中,$D$,$E$,$F$ 分别为 $AB$,$BC$,$CA$ 的中点,若 $\triangle ABC$ 的周长为 $36\mathrm{cm}$,面积为 $54\mathrm{cm}^2$,则 $\triangle DEF$ 的周长为
18 cm
,面积为13.5 cm²
。
答案:
18 cm 13.5 cm²
9. 梯形的上、下底的长分别是 $16\mathrm{cm}$,$23\mathrm{cm}$,一腰长为 $20\mathrm{cm}$,另一腰长为 $x\mathrm{cm}$,则 $x$ 的取值范围为
13 < x < 27
。
答案:
13 < x < 27
10. 如图,在矩形 $ABCD$ 中,点 $E$ 在 $BC$ 上,$AE = AD$,$DF\perp AE$ 于点 $F$,连接 $DE$。证明:$DF = DC$。
证明:∵
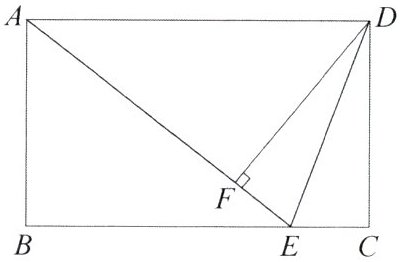
证明:∵
DF ⊥ AE 于点 F
,∴ ∠DFE = 90°。在矩形 ABCD 中,∠C = 90°,∴ ∠DFE = ∠C。在矩形 ABCD 中,AD // BC,∴ ∠ADE = ∠DEC,又 AE = AD,∴ ∠ADE = ∠AED,∴ ∠AED = ∠DEC。又 ∵ ∠DFE = ∠C = 90°,DE 是公共边,∴ △DFE ≌ △DCE (AAS),∴ DF = DC。
答案:
证明:
∵ DF ⊥ AE 于点 F,
∴ ∠DFE = 90°。在矩形 ABCD 中,∠C = 90°,
∴ ∠DFE = ∠C。在矩形 ABCD 中,AD // BC,
∴ ∠ADE = ∠DEC,又 AE = AD,
∴ ∠ADE = ∠AED,
∴ ∠AED = ∠DEC。又
∵ ∠DFE = ∠C = 90°,DE 是公共边,
∴ △DFE ≌ △DCE (AAS),
∴ DF = DC。
∵ DF ⊥ AE 于点 F,
∴ ∠DFE = 90°。在矩形 ABCD 中,∠C = 90°,
∴ ∠DFE = ∠C。在矩形 ABCD 中,AD // BC,
∴ ∠ADE = ∠DEC,又 AE = AD,
∴ ∠ADE = ∠AED,
∴ ∠AED = ∠DEC。又
∵ ∠DFE = ∠C = 90°,DE 是公共边,
∴ △DFE ≌ △DCE (AAS),
∴ DF = DC。
11. 如图,在平行四边形 $ABCD$ 中,点 $E$ 是边 $AD$ 的中点,$BE$ 的延长线与 $CD$ 的延长线相交于点 $F$。
(1)求证:$\triangle ABE\cong\triangle DFE$;
证明:
(2)试连接 $BD$,$AF$,判断四边形 $ABDF$ 的形状,并证明你的结论。
判断结果:四边形 $ABDF$ 是
证明:
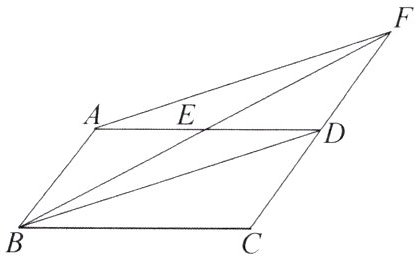
(1)求证:$\triangle ABE\cong\triangle DFE$;
证明:
∵ 四边形 ABCD 是平行四边形,∴ AB // FC。∴ ∠ABE = ∠DFE,∠EAB = ∠EDF。∵ E 是 AD 的中点,∴ AE = DE。∴ △ABE ≌ △DFE。
(2)试连接 $BD$,$AF$,判断四边形 $ABDF$ 的形状,并证明你的结论。
判断结果:四边形 $ABDF$ 是
平行四边形
。证明:
∵ △ABE ≌ △DFE,∴ AB = DF。又 ∵ AB // FD,∴ 四边形 ABDF 是平行四边形。

答案:
证明:
(1)
∵ 四边形 ABCD 是平行四边形,
∴ AB // FC。
∴ ∠ABE = ∠DFE,∠EAB = ∠EDF。
∵ E 是 AD 的中点,
∴ AE = DE。
∴ △ABE ≌ △DFE。
(2) 四边形 ABDF 是平行四边形。
∵ △ABE ≌ △DFE,
∴ AB = DF。又
∵ AB // FD,
∴ 四边形 ABDF 是平行四边形。
(1)
∵ 四边形 ABCD 是平行四边形,
∴ AB // FC。
∴ ∠ABE = ∠DFE,∠EAB = ∠EDF。
∵ E 是 AD 的中点,
∴ AE = DE。
∴ △ABE ≌ △DFE。
(2) 四边形 ABDF 是平行四边形。
∵ △ABE ≌ △DFE,
∴ AB = DF。又
∵ AB // FD,
∴ 四边形 ABDF 是平行四边形。
12. 在四边形 $ABCD$ 中,$AD// BC$,且 $AD > BC$,$BC = 6\mathrm{cm}$,$P$,$Q$ 分别从 $A$,$C$ 同时出发,$P$ 以 $1\mathrm{cm/s}$ 的速度由 $A$ 向 $D$ 运动,$Q$ 以 $2\mathrm{cm/s}$ 的速度由 $C$ 出发向 $B$ 运动,几秒后四边形 $ABQP$ 是平行四边形?
解:设 t s 后,四边形 APQB 为平行四边形,则 AP = t,QC = 2t,BQ = 6 - 2t。因为 AD // BC,所以 AP // BQ,根据一组对边平行且相等的四边形是平行四边形知:AP = BQ,即 t = 6 - 2t,解得
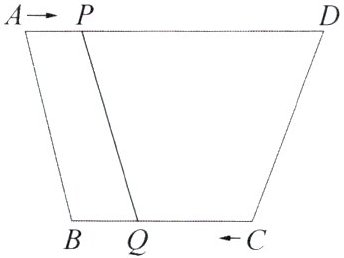
解:设 t s 后,四边形 APQB 为平行四边形,则 AP = t,QC = 2t,BQ = 6 - 2t。因为 AD // BC,所以 AP // BQ,根据一组对边平行且相等的四边形是平行四边形知:AP = BQ,即 t = 6 - 2t,解得
t = 2
,当 t = 2 时,AP = BQ = 2 < BC < AD,符合条件。综上所述,2 s
后四边形 ABQP 是平行四边形。
答案:
解:设 t s 后,四边形 APQB 为平行四边形,则 AP = t,QC = 2t,BQ = 6 - 2t。因为 AD // BC,所以 AP // BQ,根据一组对边平行且相等的四边形是平行四边形知:AP = BQ,即 t = 6 - 2t,解得 t = 2,当 t = 2 时,AP = BQ = 2 < BC < AD,符合条件。综上所述,2 s 后四边形 ABQP 是平行四边形。
查看更多完整答案,请扫码查看


