2025年暑假作业完美假期生活八年级数学湖南教育出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业完美假期生活八年级数学湖南教育出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 将一张矩形的纸对折两次,然后剪下以折点为顶点的角,剪下的图形展开后一定是
菱形
.
答案:
菱形
8. 如图,AB,CD相交于点O,OC=2,OD=3,AC//DB,EF是△ODB的中位线,且EF=2,则AC的长为____
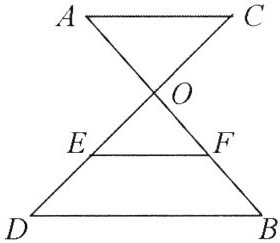
$\frac{8}{3}$
____.
答案:
$\frac{8}{3}$
9. 若矩形的对称中心到两边的距离差为4cm,周长为56cm,则矩形的边长分别为
10 cm,18 cm
.
答案:
10 cm,18 cm
10. 多边形的内角和与某一个外角的度数总和是1350°,求多边形的边数.
答案:
解:设这个外角度数为$x^{\circ}$,根据题意,得$(n - 2)×180 + x = 1350$,解得:$x = 1350 - 180n + 360 = 1710 - 180n$,由于$0 < x < 180$,即$0 < 1710 - 180n < 180$,解得$8.5 < n < 9.5$,所以$n = 9$。故多边形的边数是 9.
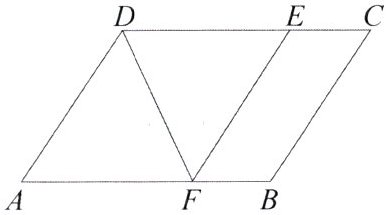
11. 如图所示,DF是平行四边形ABCD中∠ADC的平分线,FE//AD交DC于点E.
(1)四边形AFED是菱形吗?请说明理由.
答:(
(2)如果∠A=60°,AD=5,求四边形AFED的面积.
答:(
(1)四边形AFED是菱形吗?请说明理由.
答:(
平行四边形AFED是菱形,理由略
)(2)如果∠A=60°,AD=5,求四边形AFED的面积.
答:(
$\frac{25\sqrt{3}}{2}$
)
答案:
(1) 平行四边形 AFED 是菱形,理由略.
(2) $\frac{25\sqrt{3}}{2}$
(1) 平行四边形 AFED 是菱形,理由略.
(2) $\frac{25\sqrt{3}}{2}$
12. 如图,在正方形ABCD中,E为AD上一点,BF平分∠CBE交CD于点F,试证明BE=CF+AE.
证明:延长 DA 至点 G 使
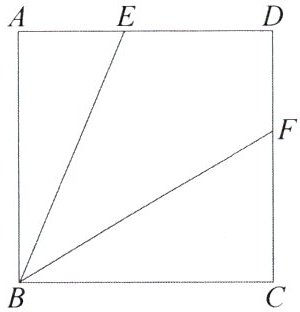
证明:延长 DA 至点 G 使
$AG = CF$
,连接 BG. 在$\triangle ABG$和$\triangle CBF$中,$\because$ $CF = AG$
,$\angle C = \angle BAG$,$CB = AB$,$\therefore$ $\triangle ABG \cong \triangle CBF$
,$\therefore$ $\angle BFC = \angle BGA$
,$\angle CBF = \angle ABG$.$\because BF$平分$\angle CBE$交 CD 于点 F,$\therefore$ $\angle CBF = \angle EBF$
,$\therefore$ $\angle ABG = \angle EBF$
.$\because AB // DC$,$\therefore$ $\angle ABF = \angle BFC$
,$\therefore$ $\angle EBG = \angle BFC$
.$\therefore$ $\angle EBG = \angle BGA$
.$\therefore$ $BE = GE$
,$\therefore$ $BE = CF + AE$
.
答案:
证明:延长 DA 至点 G 使$AG = CF$,连接 BG. 在$\triangle ABG$和$\triangle CBF$中,$\because CF = AG$,$\angle C = \angle BAG$,$CB = AB$,$\therefore \triangle ABG \cong \triangle CBF$,$\therefore \angle BFC = \angle BGA$,$\angle CBF = \angle ABG$.$\because BF$平分$\angle CBE$交 CD 于点 F,$\therefore \angle CBF = \angle EBF$,$\therefore \angle ABG = \angle EBF$.$\because AB // DC$,$\therefore \angle ABF = \angle BFC$,$\therefore \angle EBG = \angle BFC$.$\therefore \angle EBG = \angle BGA$.$\therefore BE = GE$,$\therefore BE = CF + AE$.
查看更多完整答案,请扫码查看


